Solution 2

1. The associativity and distributivity axioms follow from the diagrams

         

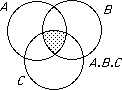
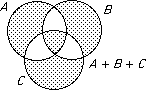
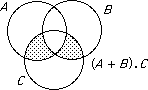
   The zero element is the empty set and each element is its own additive inverse.
   The set S itself is the multiplicative identity and is the only element with a multiplicative inverse.

   With A + B = A ∪ B we do not get a ring. The only thing that goes wrong is additive inverses.

2. Let u, v be the vectors (x₁ , y₁ , z₁) and (x₂ , y₂ , z₂).
   The product of the corresponding "pure quaternions"
   x₁ i + y₁ j + z₁ k and x₂ i + y₂ j + z₂ k is
   (x₁x₂ + y₁y₂ + z₁z₂ + (y₁z₂ - z₁y₂)i + (z₁x₂ - x₁z₂)j + (x₁y₂ - y₁x₂)k
   and this corresponds to u.v + u × v.

   The only thing that stops (R³, +, ×) being a ring is that × is not associative.
   To see this observe that (u × v) × w is perpendicular to u × v and so in the plane spanned by u and v, while u × (v × w) is perpendicular to v × w and so in the plane spanned by v and w. It is then easy to find a counterexample.

3. This is an ideal (and hence a subring) since it is generated by x².

   Check it directly [using the fact that if p(1) = q(1) = 0 then (p - q)(1) = 0 and p(1)r(1) = 0 for any polynomial r] or (cleverer!) observe that this is the ideal < x - 1 > generated by the polynomial x - 1.

4. It is easy to check the axioms. The multiplicative inverse of a + b√2 is a/(a² - 2b²) - b/(a² - 2b²)√2.

5. This is a ring of order 4 but (x + 1)² = 0 and so it has a zero divisor and is not a field.

   As usual, this is a commutative ring with identity and so we need only find multiplicative inverses.

   1^-1 = 1 and 2^-1 = 2 since -1 = 2 the "rule" gives x(x + 2) = 1 and we have inverses for two more elements. Squaring this gives (x + 1)(2x + 2) = 1 and so we have two more. Also -x(-x - 2) = 1 and this gives 2x(2x + 1) = 1 and this is the last pair.

   A cleverer way to work is to observe that powers of x generate the eight non-zero elements of the ring and then (x^m)^-1 = x^8-m.

6. If the additive order of an element a is m = pq then (writing 1 + 1 = 2, etc) we get ma = 0 = p.qa and so p and qa are zero divisors. The only way of avoiding this is for m to be a prime number.

   The order of any non-zero element is then the same as the order of 1.

7. There is a choice of p elements for each coefficient and hence there are p^k elements. Since the multiplication rule tells us p(x) = 0 in this ring, if we can split p(x) as a product of two lower degree polynomials, these elements of the ring will be zero-divisors and so we will not have a field.

   In fact, if the polynomial p(x) cannot be factorised ("is irreducible") then using the "rule" p(x) = 0 will give a field.

   If the polynomial x² - x - 1 ∈ Z₃[x] could be factored it would have to have linear factors and hence would have a root. But it is easy to check that substituting x = 0, 1, 2 will not give 0.