Rings and Fields

Solution 4

  1. It is easy to verify the conditions that I ∩ J is an ideal.

    An element of IJ is of the form i1j1 + i2j2 + ... + ikjk and each of these terms is in both I and J and hence in I ∩ J.

    If I = < 4 > in Z and J = < 6 > then all products ij ∈ IJ are divisible by 24. Thus IJ = < 24 >.
    If an ideal contains both I and J all its elements must be divisible by 12. Thus I ∩ J = < 12 >.
    The integer 2 ∈ I + J and it is easy to see that all elements of I + J are divisble by 2. Thus I + J = < 2 >.
    More generally, If I = < m > in Z and J = < n > then IJ = < mn > , I ∩ J = < lcm(m, n) > and I + J = < gcd(m, n > .


  2. The proof is similar to that showing that Z is a principal ideal domain. It is equivalent to the group theoretic result that any subgroup of a cyclic group is cyclic.
    To find all the ideals of Zn (or subgroups of this cyclic group) take the ideals generated by all the divisors of n.
    For example, Z12 has subgroups generated by 1, 2, 3, 4, 6 and 12 = 0 of orders (respectively) 12, 6, 4, 3, 2 and 1.


  3. As groups 2Z and 3Z are both infinite cyclic groups generated by 2 and 3 respectively.
    Any ring homomorphism would have to take an additive generator to an additive generator and thus map 2 to ±3. However 22 = 4 would then have to map to 6 ≠ (±3)2.

    A suitable group isomorphism is 1 ↦ (1, 1). Note that since 2, 3 are coprime the (additive) order of (1, 1) = 6.
    Then an element a = (1 + 1 + ... + 1) maps to (a, a) and b maps to (b, b). The product ab maps to (ab, ab) which is where it has to go to be a ring isomorphism.

    More generally, the same proof works for any pair of integers m, n which are coprime.


  4. You need to verify that the map is well-defined. If m = n mod 12 then 12 divides m - n and so 4 divides m - n and so the image of m and n in Z4 is the same. The other properties follow easily. Its kernel is the ideal generated by 3.

    This "well-definition" fails working modulo 14. For example 2 = 16 mod 14 but not modulo 7. This means you get problems with the homomorphism property. For example 8 ↦ 0 but 8 + 8 = 2 ↦ 2 ≠ 0 + 0.


  5. Invariance of multiplication fails for the first and invariance of addition fails for the third. Note that since C is a field the kernel of any homomorphism is either {0} or C and so these clearly cannot be homomorphisms.
    The second is an isomorphism from C to C as you can verify.
    The fourth is not a homomorphism since, for example, 1 ↦ i but 12 ↦ 1 ≠ i2 = -1.


  6. The product of units is a unit and so the set Un forms a multiplicative group. We'll write them as products of cyclic groups Ci
    U2 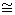C1 , U3 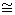C2 , U4 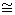C2 , U5 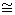C4 , U6 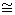C2 , U7 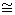C6 , U8 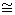C2 × C2 , U9 = C2 × C3 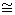C6 , U10 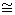C4 , ...
    The pattern you should notice is that if n is prime the group Un 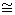Cn-1 . Then from Question 3 above if m, n are coprime Umn 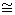Um × Un and that should enable you to take the calculation quite far.


  7. A ring homomorphism from Z12 onto Z4 will have the ideal < 3 > as kernel and is the map of Qu 4 above.
    Look at the (additive) orders of elements to conclude that the only homomorphism is x ↦ 0 for all x.
    One can only get a homomorphism from Zm onto Zn if n divides m and then it is the map x ↦ x mod n.


  8. There is only one possible addition table for a ring {0, 1} of order 2 and then either 1.1 = 0 or 1.1 = 1 give two rings.

    If the additive group is cyclic every element is of the form na for some integer n and the (ma).(na) = (mn)a2 and so if you know a2 the multipication is determined.

    The additive group of a ring of order 3 must be cyclic so R = {0, a, 2a}. Then we can either take a2 = 0 or a2 = a. If we take a2 = 2a then we have (2a)2 = 4a2= 2a and so if we swap the generators a and 2a we get isomorphic rings. Thus there are two possible rings of order 3

    For rings of order 4 with a cyclic additive group {0, a, 2a, 3a} we have a choice of 0, a or 2a for a2. Choosing a2 = 3a gives a ring isomorphic to the a2 = a case.
    There are in fact eight rings whose additive group is the Klein 4-group.