Exercises 3

1. What is the subring of R generated by 1? What is the sub-field of R generated by 1 ?
   What are the subring and subfield of R generated by √2 ? What is the ideal of R generated by √2 ?

   Solution to question 1

2. Let R be the Boolean ring of Exercises 2 Question 1. Let A be a subset of S.
   Describe the subring of R generated by the element A.
   Describe the ideal of R generated by A.

   Solution to question 2

3. If R is a commutative ring with identity whose only ideals are {0} and R, prove that R is a field.

   If R is a commutative ring with identity, do the non-invertible elements of R form an ideal? Prove this or find a counterexample.

   Solution to question 3

4. Let p = x³ + 5x - 2 and q = x² + 3 be polynomials in R[x]. Find the gcd of p and q and use the Euclidean algorithm to write it in terms of p and q.

   Solution to question 4

5. Write 2 + i = (1 + i)q + r in the Gaussian integers with N(r) < N(1 + i) in four different ways.
   Find examples of pairs of Gaussian integers which lead to three different and two different quotients and remainders.
   Are the quotient and remainder on dividing one Gaussian integer by another ever unique?

   Solution to question 5

6. The lowest common multiple (lcm) of two integers a, b is the smallest (in absolute value) integer divisible by them both.
   Prove that ab = ±gcd(a, b)lcm(a, b).
   [Hint: write a and b as products of primes.]
   Formulate the corresponding result for polynomials over a field and for the Gaussian integers.

   Solution to question 6

7. When one uses the Euclidean algorithm to write the gcd(a, b) = ax + by one may have a choice for x and y.
   For example, if a = 15 and b = 12 then d = gcd(a, b) = 3 = 1a + (-1)b = (-3)a + 4b = ...
   If we can write d = ax1 + by1 and d = ax2 + by2 what is the connection between the pairs x1 , y1 and x2 , y2 ?

   Solution to question 7

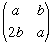8. Let R be the set of real matrices of the form . Prove that R is a subring of the ring of all real matrices.
   If we insist that the entries of R are rationals, prove that R is then a field.
   [Hint: a matrix with entries in a field is invertible if its determinant is non-zero.]

   If the entries of R are taken from the ring Z₃, prove that R is a field with 9 elements.
   Find some more primes p such that if we take the entries of R to be in the ring Z_p we get a field with p² elements.
   If you have the time (and the inclination), experiment with matrices of the form 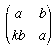for different values of k to make other fields of order p².

   Solution to question 8