Exercises 5

1. We have seen that the polynomials x² + 1, x² + 2x + 2 ∈ Z₃[x] are irreducible. Find a third irreducible monic quadratic polynomial and prove that the field it defines is isomorphic to the field determined by the other two.
   The polynomials x³ + x² + 1, x³ + x + 1 ∈ Z₂[x] are irreducible. Find an isomorphism between the two fields of order 8 they determine.

   Solution to question 1

2. Prove that if p is prime there are ¹/₂ p(p - 1) irreducible quadratic monic polynomials in Z_p[x].
   Find a formula for the number of irreducible cubic monic polynomials.

   Solution to question 2

3. Let F be a field of characteristic p. Prove that the map r ↦ r^p is a ring homomorphism.
   [You will need to use the fact that if p is prime the binomial coefficient _pC_r is divisible by p for 0 < r < p. Can you prove this?]
   The above is called the Frobenius map introduced by the German mathematician Georg Frobenius (1849 to 1917).

   Solution to question 3

4. Let f be a ring homomorpism from R onto S with kernel the ideal I. Prove that f defines a one-one correspondence between the ideals of R which contain I and the ideals of S.
   This result is called the Correspondence Theorem for Rings.

   Solution to question 4

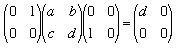5. Let R be the ring of 2 × 2 matrices with entries in a field F. Verify that . Find other similar expressions and deduce that the two-sided ideal generated by a single matrix is either {0} or the whole ring.
   A ring with only these two ideals is called simple.

   Solution to question 5

6. Find an element with multiplicative order 8 in the field Z₃[x]/ < x² + 1 > and deduce that the ring of units is indeed cyclic.
   Find the inverse of the element x in the field Z₃[x]/ < x³ + 2x + 1 > of order 27.
   Hence or otherwise find the multiplicative order of the element x in this field.
   How many elements with multiplicative order 26 are there in this field?

   Solution to question 6

7. Let R be the ring Z₆[x]. How many roots does the polynomial x² + x have in R? How can this happen with a quadratic?

   Solution to question 7

8. Fermat's Little Theorem states that if p is prime then a^p = a mod p for any integer a. Prove that the polynomial x^p - x has p roots in Z_p .
   Prove that the polynomial x^pk- x has p^k roots in a field with p^k elements.

   Solution to question 8