Finite rotation groups in 3 dimensions

The main result of this section is to classify all such groups.

A finite symmetry group cannot contain translations, glides or screws and so arguing as before, such a group must fix some point which we may as well take as the origin. We are then reduced to considering the linear case.

We start with groups of rotations and with the following result about linear groups.

Theorem
Any finite subgroup of SO(3) is either a cycle group C_n a dihedral group D_n or one of the groups of a Platonic solid.

Proof
Let G be a finite subgroup of SO(3) with order n.
Then G acts on the unit sphere S and each rotation has two fixed points: its poles. We will look at the set of all poles on S (a finite set).

Lemma 1
Every element of G maps a pole to a pole.

Proof of lemma
If p is a fixed point of an element g ∈ G and h is any element of G, then hp is a fixed point of hgh ^-1 ∈ G and hence is a pole.

We divide the set of poles into orbits: subsets of the form Gp for some pole p.

Lemma 2
If p is a pole of an element of G of maximal order m then the orbit of p contains n/m elements.

Proof of lemma
The subgroup H of G which leaves p fixed has m elements. So G is a union of cosets g₁H, g₂H, ... , g_rH with r = n/m.
All the elements in a coset g_iH will move p to the same point g_ip for i = 1, 2, ... , r.
Note that if i ≠ j then g_ip ≠ g_jp since if g_ip = g_jp then g_i^-1g_jp = p and so g_i^-1g_j ∈ H and so g_i and g_j would represent the same coset.
Hence the orbit of p is the set {g₁p, g₂p, ... , g_rp} as required.

The n - 1 non-zero rotations in G consist of m - 1 rotations for each pair of poles.
That is ¹/₂ (m - 1) n/m for each orbit.
Hence n - 1 = ¹ /₂ n(∑ (m-1)/m) where the summation is over the orbits ⇒ 2 - 2 /n = ∑ (1 - 1 /m ).
Since m ≥ 2 we have 1 - 1/m > ¹/₂ and so we can only have 2 or 3 orbits if G is non-trivial.

1. The case of two orbits
   Suppose these have n/m₁ and n/m₂ elements.
   Then 2/n = 1/m₁ + 1/m₂ ⇒ 2 = n/m₁ + n/m₂ ⇒ (since m₁ and m₂ divide n) n/m₁ = n/m₂ = 1 and we have two orbits with one pole in each. This is the case when G is a cyclic group C_n generated by rotation by 2π/n.

2. The case of three orbits
   1 + 2/n = 1/m₁ + 1/m₂ + 1/m₃.
   We must have (say) m₃ = 2 ⇒ 1/m₁ + 1/m₂ = 1/2 + 2/n ⇒ (m₁ - 2)(m₂ - 2) = 4(1 - m₁m₂/n) < 4
   There are only a few possibilities:
   
   1. m₁ = 2, m₂ = m, n = 2m (This is the dihedral case)
      
   2. m₁ = 3, m₂ = 3, n = 12 (This is the tetrahedral case)
      
   3. m₁ = 3, m₂ = 4, n = 24 (This is the cube case)
      
   4. m₁ = 3, m₂ = 5, n = 60 (This is the dodecahedral case)

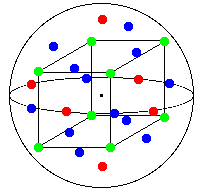Look at the case of S_d(Cube) for which |G| = 24.

Poles are:	Rotation by:	|Orbit|	Geometric feature	|G|
Red orbit	±π/2, π	6	face centres	9
Green orbit	±2π/3	8	corners	8
blue orbit	π	12	edge centres	6

Remark

Note that we are used to thinking of D_n as a group acting on R² and containing some reflections. As a subgroup of I(R³) the elements of order two are not reflections but rotations by π.