Affine theorems

In fact, many of the theorems of so-called Euclidean geometry are affine theorems. That is, their statement and proof only involve concepts which are preserved by affine transformations.
Roughly speaking, affine theorems are ones which can be proved by vector methods without using norms or dot or vector products.

Examples

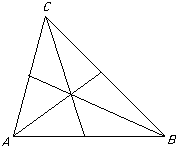
1. The medians of a triangle are coincident.

   Proof
   If the triangle has vertices a, b and c then it is easy to verify that the medians meet at the point (a + b + c) /3
   
   
   
   
   

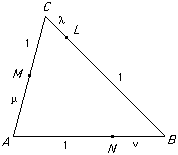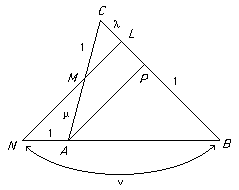
2. Ceva's theorem (due to Giovanni Ceva in about 1678)
   If the sides BC, CA, AB of a triangle are divided by points L, M, N in the ratios 1 : λ, 1 : μ, 1 : ν then the three lines AL, BM, CN are concurrent if and only if the product λμν = 1.
   
   
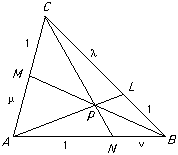   Proof
   In fact, we'll prove this using non-affine methods.
   λ = CL/LB = Δ CLA/Δ LBA = Δ CLP/Δ LBP = Δ CAP/Δ ABP.
   Similarly μ = AM/MC = Δ ABP/Δ BCP and ν = BN/NA = Δ BCP/Δ CAP and the result follows.
   
   
   
   
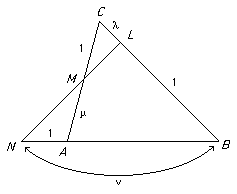3. Menelaus's theorem (due to Menelaus in about 100 AD)

   If the sides of a triangle are divided by points L, M, N in the ratios 1 : λ, 1 : μ, 1 : ν then the three points L, M, N are collinear if and only if the product λμν = -1.
   
   
   Proof
   Note that the ratio in which a point L divides an interval AB is negative if L does not lie inside AB.

   Draw AP parallel to ML. Then 1/μ = CM/MA = CL/LP and 1/ν = AN/NB = PL/LB.
   Then 1/(μν) = CL/LP . PL/LB = -CL/LB = -λ and the result follows.
   
   

1. Ceva rediscovered Menelaus's theorem and then discovered his own -- 1500 years later !

2. As in the case of an isometry, an affine transformation is determined by the image of any n + 1 independent points (ones which do not lie in an (n - 1)-dimensional affine subspace).
   In the case of an affine transformation, any n + 1 independent points can be mapped to any n + 1 independent points.
   In particular, in R² there is a unique affine transformation taking a triangle ABC into a triangle A'B'C'.

3. The usual three-way classification of conic sections into ellipses, hyperbolas and parabolas is an affine classification.
   For example, any two ellipses are related by an affine transformation.