Course MT4521 Geometry and topology
The linear groups
We shall investigate the groups which are associated with the usual (Pythagorean) metric on the vector space Rn. These are the groups which preserve this distance.
It turns out that they involve linear algebra. The reason for this is that straight lines in this geometry can be defined as the shortest paths between points in the metric and since the metric is preserved by the transformations they must then map straight lines to straight lines and we will see (eventually) that this means they involve linear maps (but rather special ones).
Definitions
A map f from Rm to Rn is called linear if it maps a linear combination of vectors to the same linear combination of the images.
That is, if u, v ∈ Rm and λ, μ ∈ R then f(λu + μv) = λf(u) + μf(v) ∈ Rn.
By fixing a basis {b1 , b2 , ... , bn } of the vector space Rn (for example, {(1, 0, 0, ... , 0), (0, 1, 0, ... , ), ... , (0, 0, ... , 0, 1)} ) we can describe the effect of such a map by its matrix. Mf = (aij) where f maps the ith basis element bi to ai1b1 + ai2b2 + ... + ainbn.
Such a transformation is a bijection if it has an inverse map f-1 or equivalently if the determinant of its matrix is non-zero.
The set of all such invertible linear transformations from the vector space Rn to itself is called the General Linear group and is denoted by GL(n, R) or GLn(R) or GL(Rn)
Note that the determinant of a matrix satisfies det(AB) = det(A) × det(B) and so is a group homomorphism from the group GL(n, R) to the group R - {0} under real multiplication. The set of all invertible transformations (or equivalently of invertible matrices) with determinant 1 is then a subgroup of GL(n, R) called the Special Linear group and denoted by SL(n, R).
Remarks
- The set of all real n × n matrices can be regarded as Rn2 and since the determinant map is a polynomial in these n2 entries it is continuous. It follows that the set GL(n, R) which is det-1(R - {0}) is an open set of Rn2 and can be thought of as having dimension n2. The set SL(n, R) satisfies one equation and so has one "degree of freedom" less and so has dimension n2 - 1.
For example, GL(1, R) is just R - {0} and so has dimension 1. SL(1, R) is the set {1, -1} and so has dimension 0.
GL(2, R) = {(a, b, c, d) ∈ R4 | ad - bc ≠ 0 } and is the set of points which "miss" the hypersurface with equation ad = bc and so is an open set in R4. The subgroup SL(2, R) = {(a, b, c, d) ∈ R4 | ac - bd = 1 } and is a 3-dimensional subset of R4.
- In general elements of GL or SL do not preserve the metric.
A linear map will in general map a rectangle to a parallelogram and so even if it manages to preserve the lengths of the sides of the rectangle, it will in general stretch the diagonals and so will not preserve all lengths.
You can think of elements of SL as preserving the "multi-dimensional volume" in Rn (area in the case n = 2) but even these will in general change lengths of some vectors.
- There are also maps from Rn to itself which do preserve the metric but which are not linear maps. Since any linear transformation maps the 0-vector to itself, a map like a translation: x
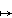 x + a for a fixed vector a, will preserve length but is not linear.
x + a for a fixed vector a, will preserve length but is not linear.
We now look at linear transformations which do preserve distance.
Definitions
We will denote the norm or length of a vector x by 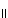 x
x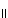 This is d(x, 0).
This is d(x, 0).
A distance preserving linear transformation T is said to be orthogonal. That is 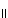 T(x)
T(x)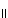 =
= 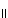 x
x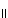 for all vectors x.
for all vectors x.
Such transformations form the orthogonal group O(n).
Remarks
- Such maps are invertible.
Proof
Since T is length preserving it can't map a non-zero vector to 0 and so the null-space has dimension 0 and T is one-one. It is a standard result about linear transformations from n dimensional spaces to n dimensional spaces that dim(null space) + dim(range) = n and so the dimension of the range of T is n and it is hence an onto map. Thus it is a bijection.

- Since T preserves lengths, it preserves angles also. This is because the angles of any triangle are determined by the lengths of its sides.
- With respect to an orthonormal basis (one whose elements are all of unit length and mutually perpendicular) the matrix of such a transformation has orthonormal columns and also orthonormal rows.
Unless we state otherwise we will usually take our basis to be orthonormal and we will blur the distinction between a transformation and the matrix representing it.
- One may prove that such a matrix satisfies AtA = AAt= I where t indicates the transpose. It then follows [since det(A) = det(At)] that (det A)2 = 1 and hence det A = ±1.
Definition
The Special Orthogonal group SO(n) is the subgroup of O(n) of elements whose matrix has determinant 1.
Remarks
- The group O(n) is the union of SO(n) and the coset K.SO(n) where K is a matrix (say)
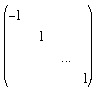 which is orthogonal with determinant -1.
which is orthogonal with determinant -1.
Since SO(n) has two cosets in O(n) it is a normal subgroup.
- Note that the subset H = {I, K} is a subgroup of O(n). In general the group O(n) is not the direct product SO(n) × H although it is equal to the cartesian product as a set.
JOC February 2010
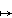 x + a for a fixed vector a, will preserve length but is not linear.
x + a for a fixed vector a, will preserve length but is not linear.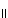 x
x
 which is orthogonal with determinant -1.
which is orthogonal with determinant -1.