Solutions 1

1. (a) Given a segment AB draw a circle centre A through B and a circle centre B through A. They meet in points C, D. Then the meet of CD and AB is the required midpoint. In fact the line CD is the perpendicular bisector of AB.
   (b) Given an angle at A, draw a circle centre A to cut off two segments AB and AC on the sides defining the angle. Use (a) to find the midpoint D of BC and AD is then the angle bisector.
   (c) Given a point A on the line, use the compass to mark off two points B, C on the line equidistant from A. Then draw the perpendicular bisector of BC as in (a) above.
   (d) Given a point A not on the line BC. Draw a circle centre A through B which then meets the line at points B and (say) D. Then construct the perpendicular bisector of BD.
   (e) Draw a perpendicular AB from the point A to the line and then take the line AC perpendicular to AB.
   (f) Draw the perpendicular bisectors of AB and AC. These meet in a point O. Then the circle centre O through A passes through B and C also.
   (g) (A tricky one!) Draw any line through A not containing the segment AB. Mark off three equal segments AC, CD, DE on the line. Join EB. Draw two lines parallel to EB through C and D and these will meet AB at points dividing it equally.
   Clearly a similar method could be used to divide AB up into any number of equal subintervals.
   (h) Given the segment AB, draw a circle centre A through B. Then marking off three points on the circle with the same radius gives the opposite end C of the diameter through B. So the line AB has been extended to CB.
   This is equivalent to building up a network of equilateral triangles!

2. We'll show that the group of rigid motions is a subgroup of Bij(R²). So we need only check that it is closed under composition and taking inverses.
   If d(x, y) = d(f(x), f(y)) and d(x', y') = d(g(x'), g(y')) then put x' = f(x) and y' = f(y) and it follows that g f also preserves length.
   Closure under inverses works similarly.

   To prove that conguence is an equivalence relation:
   The reflexive property follows from the fact that the identity map is in the group of rigid motions.
   To prove symmetry, suppose that F₁ and F₂ are conguent and that f(F₁) = F₂ with f a rigid motion. Then f ^-1 is also in the group and f ^-1(F₂) = F₁ and the result follows.
   If F₂ and F₃ are congruent and g(F₁) = F₂ then g f is a congruence between F₁ and F₃ and transitivity follows.

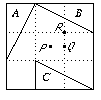3. Rotation by -π/2 about the centre P maps triangle A to triangle B.
   Rotation by π about the centre Q maps triangle B to triangle C.
   Rotation by +π/2 about the centre R maps triangle A to triangle C.

   Note that the third is the composite of the first two. The composite of two rotations is always another rotation.

4. Rotating three times by 60° gives a rotation by 180°. The only problem is to identify the point about which the rotation takes place.
   In the first case the rotation is about the mid-point of AC, in the second it is about the point C.

5. Since a triangle is determined by the lengths of its sides, any map which preserves all lengths also maps all triangles congruently. But the triangle determines the size of its angles and so these too are preserved.

   A map like (x, y) (2x, 2y) preserves angles but does not preserve lengths.

6. Since det(A.B) = det(A).det(B) the determinant is a group homomorphism from GL to R - {0}

   SL is the kernel of this homomorphism and hence is a normal subgroup of GL.

7. Suppose that A has orthonormal columns a_i. Then A^t has orthonormal rows a_i^t. The (i, j)th entry of the product A^tA is then a_i^ta_j and this is 1 if i = j and 0 otherwise. Thus A^tA = I
   Conversely if A^tA = I then A has orthonormal columns and is orthogonal.

   If A^tA = I then A^t is the left inverse of A and since the left inverse of a square (finite-dimensional) matrix is also a right inverse, it follows that AA^t = I also. That is, A^t has orthonormal columns and so A has orthonormal rows.

   [Proving this in a specific case -- even 2 × 2 -- is harder than you might think!]
   Since either b or d ≠ 0 assume (without loss of generality) that b ≠ 0.
   Then a = -cd/b and a² + c² = (cd/b)² + c² = 1 ⇒ c²(d² + b²) = b² ⇒ c² = b².
   Hence a² + b² = a² + c² = 1 and c² + d² = b² + d² = 1.
   If c = b then ab + cd = 0 ⇒ ac + bd = 0 and if c = -b then ab + cd = 0 ⇒ a(-c) + (-b)d = 0 ⇒ ac + bd = 0.