Solutions 4

1. Let A be generated by r₁ : a rotation by 2π/n about a and let B be generated by r₂ : a rotation by 2π/n about b. Let g be any isometry that maps a to b. (for example T_b-a)
   Then r₂ = g ^-1r₁g (just check the fixed point.) and so B = g ^-1Ag as required.
   By definition the subgroups C_n are generated by such rotations and so are conjugate.
   To prove that any two copies of D_n are conjugate, suppose that they are generated by rotations about points a, b and reflections in a lines l containing a and m containing b.
   This time choose a symmetry which maps a 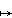b and l 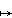m (for example, T_b-a followed by a suitable rotation about b) and proceed as before.
   [Note that Leonardo's Theorem is really a classification of the finite subgroups of O(2) up to conjugacy by elements of O(2) .]
   Since conjugation by any element preserves the determinant, we cannot have D₁ (determinant = -1) conjugate to C₂ (determinant = +1).

2. If a subgroup of I(R) contained translations by arbitrarily small amounts it would not be discrete. Hence there is a translation T_m by some smallest number m. Then if there is a translation T_k by an amount which was not a multiple of m, we could write k = am + r with |r| < |m| and T_r would also be in the subgroup, giving a contradiction.

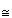3. If the subgroup is generated by the smallest translation T_m then it is an infinite cyclic group C_∞ ( Z under +).
   Otherwise it will also contain a reflection and conjugating this reflection by the smallest translation will give a reflection in a different point and it may then be generated by these two reflections whose product will be the translation.

   The frieze groups (i) and (ii) are each generated by a single element of infinite order and hence are 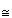C_∞.
   Note that although the two subgroups are isomorphic as groups, they are not conjugate subgroups in the group of all symmetries of the strip.
   The group (iii) is generated by a translation and an element of order 2 (reflection in the horizontal) which commutes with the translation and hence is C_∞ × D₁.
   The group (iv) is generated by a pair of reflections (one through the centre of each symmetric motif and the other between each pair of motifs).
   The group (v) is generated by a pair of elements of order 2 (this time half turns, one about the centre of each motif and the other about a point between each pair of motifs).
   The group (vi) is generated by a pair of elements of order 2 (a reflection through the centre of each motif and a half turn about a point between each pair of motifs).
   The group (vii) is generated by the same pair of elements as in any of the previous three cases (giving the group D_∞) together with reflection in the horizontal which commutes with everything else. Hence the group is 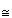D_∞ × D₁.

4. Inversion in a is a rotatory reflection: reflection in any plane followed by rotation by π about an axis perpendicular to the plane.
   Following this with a rotation about the same axis gives a rotatory reflection. Hence any rotatory inversion is a rotatory reflection.
   The converse works similarly.

5. 1. To check the homomorphism property θ(AB) = θ(A) θ(B) for all A, B ∈ O(3) we must verify that det(AB) AB = det(A) A det(B) B and that det(AB) = det(A) det(B). The second of these is the standard property of the determinant while the first follows from the fact that multiplication by the scalar det(B) (which is ±1) commutes with the matrix A.
      It is easy to check that θ is a bijection.

   2. The full symmetry group of X (which is a subgroup of O(3)) is mapped by θ to a subgroup of SO(3) × < J >.
      [Note that θ(J) = (I, -1) which is why we take J as the generator of the second factor.]
      This subgroup is the group S_d(X) × < J >.
      
   
   

6. The twelve points are (±a, ±1, 0), (0, ±a, ±1), (±1, 0, ±a). We may take A to be (1, 0, a), B to be (-1, 0, a) and C to be (0, -a, 1).
   Then the distance AB is 2 and (distance AC)² = 1 + a² + (a - 1)² = 2(a² - a +1). So these are the same if a² - a +1 = 2. i.e if a is the Golden Ratio.
   These twelve points can then be used to define 20 equilateral triangles which make up the icosahedron.