The dual of the truncated octahedron has 24 triangular faces which careful consideration shows to come together to form 12 rhomboidal faces and so the dual is the rhombic dodecahedron.
The truncated octahedron and and the rhombic dodecahedron are particularly important because copies of them can be used to fill up R3 without any gaps. Consequently, they appear "in nature" as crystals of various chemical compounds. With the obvious exception of the cube, none of the other Platonic solids can do this.
The stella octangula has 24 faces, 8 vertices with 3 incident edges and 6 vertices with 8 incident edges. Hence its dual solid has 24 vertices, 8 triangular faces and 6 octagonal faces. It is a truncated cube:
Hence the symmetry groups of the stella octangular are the same as those of the cube/octahedron.
Sd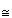 
S4 and S 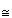S4 × < J > .
Colouring the two tetrahedra differently reduces the symmetry groups to those of the tetrahedron: Sd 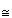A4 and S 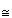S4.
Colouring the top and bottom of the dual truncated cube differently from the others will give a figure whose rotational symmetry group Sd 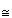D4 (the rotational symmetries of the square half-way up) and whose full symmetry group is S 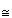D4 × < J > .
Colouring the upper and lower faces or edges of the stellar octangula will have the same effect.
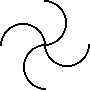whose 2-dimensional symmetry group is C4 on (say) the top face. (If you like, you can put its mirror image on the bottom face, but if you use the symbol on the bottom without reflecting it you'll get a D4.)
(b) Paint each pair of opposite faces the same colour and you'll get a D2.
(c) Paint a line on the top face and then rotate the cube by the appropriate amounts for A4 and paint the other faces to match what you get. (That's really the same as Question 2 above.)
Question: Can you mark a cube to get a D3 ? Hint: D3 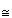S3 and remember what are permuted when you get the group Sd(C) as S4 .
On the tetrahedron, reflection in a plane containing one edge (and passing through the mid point of the opposite edge) swaps a pair of vertices and leaves the other pair fixed and so corresponds to a 2-cycle in S4. There are indeed 6 such 2-cycles and 6 edges to choose from !
Take one of the three line joining centres of opposite edges. Then a rotatory reflection (by ±π/2) about this axis is a symmetry of the tetrahedron, and there are 6 of them -- corresponding to the 6 4-cycles in S4.
The above account for all 12 of the odd permutations in S4.
The 3-cycles all have order 3 in A5 and so correspond to rotations by multiples of 2π/3. There are (5×4×3)/3 = 20 of these in A5 and on the dodecahedron there are 10 axes joining pairs of opposite vertices and 2 non-trivial rotations for each of them.
There are [(5×4)/2×(3×2)/2]/2 = 15 permutations of shape: (**)(**) in A5 and they have order 2 so correspond to rotations by multiples of π. On the dodecahedron there are indeed 15 axes joining centres of opposite edges and one non-trivial rotation for each of them.
(We use edge-length 2 to make the arithmetic easier)Each altitude of the equilateral triangular faces has length √3. So the area of the base √3.
To calculate the height of the tetrahedron, consider the triangle ABE containing one side and the midpoint of the opposite side. This triangle contains the altitude h of the tetrahedron and has sides √3, √3 and 2. Since the length of the altitude EF is √2 (by Pythagoras) the area of the triangle is √2 and since the area is also √3 /2 h we have h = √8/√3. So the volume is 1/3 × √3 × √8/√3 = 1/3 √8.
Since the "top half" of the octahedron is a pyramid, we may argue similarly to find its height = √2. Since the base has area 4, the volume of the pyramid is 4/3 √2 and the volume of the octahedron is 8/3 √2.
Cutting 4 small tetrahedra (each with volume 1/24 √8 ) off the bigger one leaves behind a octahedron with edge-length 1 and so this has volume 1/3 √8 - 4/24 √8 = 1/3 √2 which is (as it should be) 1/8 of the volume calculated above.