Course MT4521 Geometry and topology

Solutions 7

  1. λ1a1 = a1 - λ2a1 - λ3a1 ... - λra1 and so λ1a1 + λ2a2 + ... + λrar = a1 + λ2(a2 - a1) + λ3(a3 - a1) + ... + λr(ar - a1) and so the span is the translation by a1 of the linear subspace spanned by { (a2 - a1), (a3 - a1), ... , (ar - a1) }.

  2. Suppose we have μ2(a2 - a1) + μ3(a3 - a1) + ... + μr(ar - a1) = 0. Then -(μ2 + μ3 + ... + μr)a1 + μ2a2 + ... + μrar = 0 and since the sum of the coefficients is 0 it follows that μ2 = μ3 = ... = μr = 0 and so the given set is linearly independent.

    To prove that (a1, 1), (a2, 1), ... , (ar , 1) are linearly independent, suppose that λ1(a1, 1) + λ2(a2, 1) + ... + λr(ar , 1) = 0 in Rn+1. Then we have λ1a1 + λ2a2 + ... + λrar = 0 in Rn and λ1 + λ2 + ... + λr = 0 in R and so from the definition of affine independence we have λ1 = λ2 = ... = λr = 0 and so the given set is linearly independent.

    Given two affinely independent sets { a0 , a1 , ... , an } and { b0 , b1 , ... , bn } in Rnthe sets { a1 - a0 , ... , an - a0 } and { b1 - b0 , ... , bn - b0 } are linearly independent and so there is a unique linear map L taking one to the other. Then the map Tb0 comp L compT-a0 is the required affine map. It is easily seen to be unique.

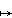
  3. As in the Question 3 of Exercises 3, let M be the matrix with A ∈GL(n, R). Then M maps a column to a similar column and so acts on this affine subspace by goesto where y = Ax + (a1, ... , an) Hence M acts as an affine transformation.
    As in the last example, the n + 1 affinely independent points give n + 1 linearly independent points whose image determines a matrix and hence the map.

  4. Suppose f is Ta comp L with L linear. Then f(λ1a1 + λ2a2 + ... + λrar) = a + λ1L(a1) + λ2L(a2) + ... + λrL(ar).
    λ1f(a1) + λ2f(a2) + ... + λrf(ar) = λ1(a + L(a1)) + λ2(a + L(a2)) + ... + λr(a + L(ar)) which is the same since λ1 + λ2 + ... + λr = 0.
    The centroid of { a1 , a2 , ... , ar } is 1/n(a1 + a2 + ... + ar) and so this is mapped to 1/n(f(a1) + f(a2) + ... + f(ar)) as required.

  5. A line joining the midpoints of two sides of a triangle is parallel to the third side.


    Hence the pair of sides shown is parallel. Similarly for the other pair of sides.


    The centroid of the quadrilateral is 1/4 (a + b + c + d). This is also the centroid of the parallelogram: 1/4 [(a + b)/2 + (b + c)/2 + (c + d)/2 + (d + a)/2] whose centroid is the meet of its diagonals.
    This result does hold in R3 also.

  6. To find a fixed point, we solve (a + L comp λI)x = x. That is (I - λL)x = a with L ∈ O(2). But L can only have eigenvalues of ±1 and so the transformation I - λL is invertible unless λ = ±1 (when the transformation will be an isometry). Hence we can solve the equation to find a unique fixed point.

  7. Take a square ABCD on AB and two possible squares A'B'C'D' and A'B'C''D'' on A'B'.
    Note that similarity transformations map squares to squares.
    There is a unique affine map taking ΔABC to ΔA'B'C' and another (opposite) affine map taking ΔABC to ΔA'B'C'' and these are the required pair of similarities.

  8. If you think of the cards as extending out to the faces of a cube, you get the picture on the right.
    So (as in Exercises 5 Question 3(c)) the rotational symmetry group is A4 (consisting of three rotations by π about the centres of faces and 8 rotations by ±2π/3 about the diagonals (but no rotations by ±π/2 about the faces or rotations about the centres of edges).
    Since the figure has central symmetry, the full rotation group is A4 × < J >.