Exercises 4

1. If A and B are two subgroups of I(R²) each generated by a rotation by 2π/n (about different points of R²), then prove that A and B are conjugate subgroups.
   (i.e. for some g ∈ I(R²) we have A = g^-1Bg.)
   Deduce that although there are many different subgroups of I(R²) isomorphic to C_n they are all conjugate.

   Prove the same result for subgroups isomorphic to D_n.

   Prove that although the subgroups D₁ and C₂ are isomorphic as groups, they are not conjugate subgroups of I(R²).

   Solution to question 1

2. A subgroup of symmetries of a set S is called discrete if there is some distance m such that every element of S is either fixed or moved by at least m by every element of G.
   If G is a discrete subgroup of I(R), prove that G contains a translation T by a minimum distance and that every translation in G is a power of T.

   Solution to question 2

3. Prove that there are two infinite discrete subgroups of the group I(R), one generated by a translation (which we will call C_∞ Z under addition) and the other generated by a pair of reflections (which we will call D_∞).

   Prove that the Frieze groups (i), ... , (vii) considered earlier are (respectively) isomorphic to C_∞, C_∞, D_∞, D_∞, D_∞, C_∞ × D₁, D_∞ × D₁.

   Solution to question 3

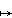4. Inversion in a point a ∈ R³ or reflection in a is the map x 2a - x.
   A rotatory inversion is rotation about a line L followed by inversion in a point of L.
   Show that every rotatory reflection is a rotatory inversion and vice versa.

   Solution to question 4

5. 1. Define a map θ from O(3) to the direct product SO(3) × {±1} by
      θ(A) = ( (det(A).A, det(A) ).
      i.e. θ(A) = ( A, 1 ) if A ∈ SO(3) and ( -A, -1 ) if A ∉ SO(3).
      Prove that θ is a group isomorphism.

   2. If X is a subset of R³ with -X = X (i.e. x ∈ X if and only if -x ∈ X) prove that the group S(X) of all symmetries of X is isomorphic to S_d(X) × < J > where S_d(X) is the subgroup of direct symmetries of X and < J > is the group of order 2 generated by J 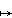: x -x.
      
   
   Solution to question 5
   
   
6. Three identical cards with dimensions 2 × 2a for a a real number are assembled as shown with their centre lines along the axes. Write down the coordinates of the twelve corners of the cards.
   Show that if the number a is the Golden ratio φ = ¹/₂ (1+√5) then the distance AB is equal to the distance AC and deduce that the twelve points are at the vertices of an icosahedron.

   Solution to question 6