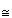Exercises 6

1. The embedding of a regular tetrahedron in a cube shown on the right, gives a map from the full symmetry group of the tetrahedron: S(T) S₄ to the full symmetry group of the cube: S(C) 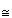S₄ × < J > .
   Identify the image and kernel of this homomorphism.

   Solution to question 1

2. Show that the 60 indirect symmetries of the dodecahedron consist of 15 reflections and 45 rotatory reflections.

   Solution to question 2

3. Show that the groups C₂ , C₁ × < J > and C₂ C₁ are isomorphic but that they are not conjugate subgroups of I(R³).

   Solution to question 3

4. Show that the group of rotations of a regular prism P_n = P × I 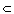R³ with P a regular polygon and I the unit interval, is the dihedral group D_n.
   What is its full symmetry group ?

   A square antiprism (with two parallel square faces and eight isosceles triangles for the others) is as shown on the right:
   Find its direct and full symmetry groups.

   Solution to question 4

5. Describe figures in R³ whose direct symmetry groups are each of the examples in the classification of rotational symmetry groups and which have no opposite symmetries.
   [Hint: think about "painting designs" on the faces of some of the figures which do have opposite symmetries.]

   Describe figures whose full symmetry groups are G × < J > with G each of the possible direct symmetry groups and where J is central inversion.

   Solution to question 5

6. Describe a figure in R³ whose full symmetry group is the mixed group D_nC_n.
   Find a figures whose full symmetry group is D_2nD_n.
   Modify this last two example to find a figure with full symmetry group C_2nC_n.

   Solution to question 6

7. Observe that one may "fill in the gap" between the upper halves of two regular octahedra with a regular tetrahedon and deduce that one may fill the whole of space with a mixture of regular octahedra and tetrahedra.

   If you fill a large volume with this mixture, do you need more tetrahedra than octahedra, or less, or the same?

   Solution to question 7

   
   

8. Figures are formed by placing two identical oblong tiles on top of each other with their centres in the same vertical line.
   If the angles between their long axes are as shown:
      (i) 0   (ii) π/2   (iii) π/3,
   find the orders of their direct and full symmetry groups and identify these groups.

   If the upper tile is coloured white and the lower one is coloured black, determine the direct and full symmetry groups in the three cases.

   Solution to question 8