Exercises 8

1. Let f be the element f = (ax + b)/(cx - a) with a, b ∈ R, a² + bc > 0. Find the order of f in the projective group PGL(2, R).
   Let g be the element g = (x -1)/x and let h be h = 1 - x. Find the orders of g and h in PGL(2, R).
   Calculate the elements of the subgroup of PGL(2, R) generated by g and h. What is the group?

   Solution to question 1

2. Show that any three distinct points on a projective line can be mapped to any three distinct points on a second line by positioning the lines suitably in a plane and projecting from a point not on either line.

   Solution to question 2

3. Show that any four points (no three on a line) in RP² can be mapped to any other four such points by a projective transformation.
   [Hint: Show first that one can map [α, 0, 0], [0, β, 0] and [0, 0, γ] to three of the points. Then choose α, β, γ so that [1, 1, 1] is mapped to the fourth point.]

   Solution to question 3

4. Given any vector space V over a field F, we can form its associated projective space P(V) by using the construction from lectures:
   P(V) = V - {0}/~ where ~ is the equivalence relation u ~ v if u = λv for u, v ∈ V - {0} and λ ∈ F.
   Let F be a finite field with p^k elements where p is a prime number.
   Prove that a projective line over F has p^k + 1 points on it and that in general if V has dimension n over F, then |P(V)| = (p^kn - 1)/(p^k - 1).

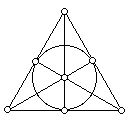
   Deduce that if |F| = 2 and n = 3 we get a projective plane with 7 points.
   (The picture on the right represents such a plane. It has 7 points and 7 lines: each point lies on 3 lines and each line contains 3 points. One of the lines is represented by a circle.)

   Describe how one could construct projective planes with 13 points and with 21 points.
   
   
   Solution to question 4
   
   

5. Prove Pappus's theorem (about 320 AD):
   If the vertices of a hexagon lie alternately on two lines, then the meets of opposite sides are collinear.

   [Hint: Project two of the meets to points on the line at infinity.]

   Solution to question 5