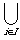Compactness

The property of being a bounded set in a metric space is not preserved by homeomorphism. For example, the interval (0, 1) and the whole of R are homeomorphic under the usual topology. So to generalise theorems in Real analysis like "a continuous function on a closed bounded interval is bounded" we need a new concept.

This is the idea of compactness. We will give a definition which applies to metric spaces later, but meanwhile, phrased purely in terms of open sets we have:

Definitions
A topological space is compact if every open covering has a finite sub-covering.

An open covering of a space X is a collection {U_i} of open sets with 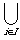U_i = X and this has a finite sub-covering if a finite number of the U_i's can be chosen which still cover X.

The most important thing is what this means for R with its usual metric.

Theorem
The interval [0, 1] is compact under the usual metric on R.

Proof
Let {U_i} be an open covering of [0, 1]. The trick is to consider the set A = {x 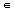[0, 1] | [0, x] can be covered by finitely many of the U_i's}. Then use the Completeness property of R to take 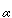to be the least upper bound of A.

Suppose 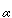< 1. Then 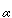is contained in some open set U_i0 and so lies in an 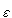-neighbourhood lying in U_i0 .
But now [0, 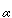- 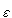/2] is covered by finitely many of the U_i's and so this collection, together with U_i0 covers [0, 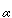+ 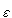/2] which contradicts the definition of .


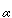A similar proof shows that any closed bounded interval of R is compact. We will see later that in fact any closed bounded subset of R (with its usual metric) is compact.

Theorem
A compact subset of R with its usual metric is closed and bounded.

Proof
If a set A 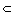R is not closed then there is a limit point p A. Then cover A by complements of closed 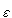-neighbourhoods of p for p = 1, ¹/₂ , ¹/₃ , ... .
For example If A = (0, 1) and p = 0 then (0, 1) = (¹/₂ ,1) 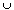(¹/₃ ,1) 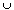(¹/₄ ,1) ...
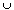We cannot take a finite subcover to cover A.

A similar proof shows that an unbounded set is not compact.


Properties of compactness

1. Continuous images of compact sets are compact.
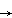   That is , if f : C Y is continuous and C is compact then f(C) is compact also.

   Proof
   Let {U_i} be an open cover of f(C). Then {f ^-1(U_i)} is an open cover of C and can therefore be reduced to a finite subcover. The corresponding collection of U_i's will be a finite sub-cover of f(C).
   
   
   Corollary
   If X is compact and ~ is any equivalence relation then X/~ is compact.

   Proof
   The natural map p: X 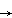X/~ is continuous and onto.
   
   
   

2. Any closed subset of a compact space is compact.

   Proof
   If {U_i} is an open cover of A 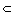C then each U_i = V_i 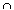A with V_i oopen in C. Then the collection {V_i} together with the open set C - A cover C and hence have a finite subcover. The corresponding U_i's then cover A.
   
   
   Corollary (The Heine-Borel theorem)
   Any closed bounded subset of R with its usual metric is compact.

   Proof
   Any such subset is a closed subset of a closed bounded interval which we saw above is compact.
   
   

   Remarks
   

   1. Note that the condition of "with its usual metric" is necessary. For example, R under the metric of Exercise 9 Question 7 has the same topology as the usual metric on R but the result fails.
      
   2. Eduard Heine (1821 to 1881) stated a version of this result in 1872. This had in fact been proved in lectures by Dirichlet in 1862. Emile Borel (1871 to 1956) published his theory of countable coverings in 1895 as part of his study of measure theory. The priority question is complicated.
      
   
   Corollary
   Any real-valued function on a closed bounded interval is bounded and attains its bounds.

   Proof
   The closed bounded interval is compact and hence its image is compact and hence is also a closed bounded subset which is in fact an interval also, by connectedness. Thus the function is bounded and its image is an interval [p, q]. It attains its bounds at points mapped to p and q.
   
   
   

3. Any compact subset of a Hausdorff space is closed.

   Proof
   Suppose C 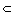X is compact. To show that X - C is open we take x 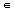X - C and try and show that x is in an open subset of X - C.
   For each y 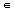C we can find disjoint open sets U_y and V_y separating x and y: x 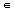U_y y 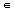V_y . The set 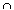U_y where the intersection is over all y 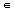C does not meet C and hence is in X - C. Unfortunately, it is not necessarily open since a topology 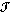is not closed under infinite intersections. However, since C is compact, we may discard all but finitely many of the V_y's and the intersection of the corresponding U_y's will be the open set we need.
   
   
   

4. Any compact Hausdorff space is also normal.

   Proof

   
   
   

5. The product of compact spaces is compact.

   This result is known as Tychonoff's theorem after Andrei Tychonoff (1906 to 1993) who proved it for a product of infinitely many spaces. Even for two spaces the proof is surprisingly tricky.

   Corollary
   The closed unit square [0, 1] 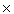[0, 1] is compact.
   Hence too are spaces like the Möbius band, Real projective palne, torus, sphere, ... made from it by identification.