Solution 1

1. The answers will depend on the way you write!
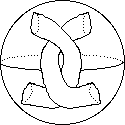
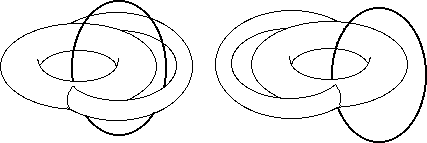   For this particular sans-serif font A R, C G I J L M N S U V W Z, D O, E F T Y, H K and the rest (B, P, Q, X) are distinct.

   Regarding the letters as having finite thickness gives some more homeomorphisms. For example P O.
   So one gets A D O P Q R, B on its own and all the rest homeomorphic to one another.
   Note that the equivalence classes are distinguished by the "number of holes".

   Making the letters 3-dimensional does not produce any further homeomorphisms.

2. To map the interval [a, b] to [c, d] take the linear map whose graph is the straight line joining the point (a, c) to (b, d).

   The same map works for the finite open intervals also.

   The map x 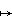tan(x) maps the finite open interval (-p/2, p/2) to the whole line R in a bijective way with the continuous inverse y 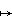tan^-1(y).

   The same map shows that any open interval of the form (a, ) or (-, b) is homeomorphic to a subinterval of (-p/2, p/2).
   Hence any open intervals are homeomorphic to finite open intervals and hence to each other.

   Similar methods show that all half-open intervals are homeomorphic to one another.

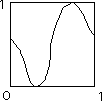3. Here is a suitable map. Note that it is not one-one.
   Similarly, the sine function maps the open interval (-, ) to the closed interval [-1, 1].

   In fact one cannot find a continuous map from the interval [0, 1] onto (0, 1) but that is hard to prove. You will see a proof later.
   
   

4. The "intertwined" two-holed torus can be considered as a sphere with two "handles" attached as shown below. Move one of the ends of the handles through the other "arch" so that the two handles are "unlinked".

   Think of the two-holed torus as made by adding a tube to a one-holed torus. Swing this round as shown below to see that the two configurations can be deformed into one another.