Then summing the coordinates of u and v and using |a + b|
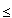 |a| + |b| in R gives the triangle inequality in d1.
|a| + |b| in R gives the triangle inequality in d1.
For d2 : |u + v|2 = |u|2 + |v|2 + 2 u.v and since u.v = cos(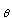 )|u||v| and cos(
)|u||v| and cos(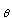 )
) 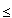 1 this is
1 this is 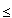 |u + v|2 and the result follows.
|u + v|2 and the result follows.
For d : the maximum of the first coordinates of u+ v
: the maximum of the first coordinates of u+ v  maximum of |coordinates of u| + maximum of |coordinates of v| and similarly for the second coordinates.
maximum of |coordinates of u| + maximum of |coordinates of v| and similarly for the second coordinates.
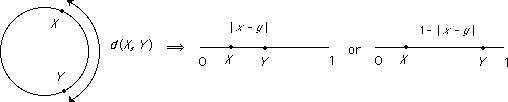
On the interval (0, 1) if |x - y| < 1/2 then d(x, y) = |x - y| otherwise it is 1 - |x - y| and so this is the same as the distance measured on a circle of perimeter 1.
The same formula does not define a metric on the closed interval [0, 1] since d(0, 1) = 0 but these two points are not the same.
d(0, pk) = 1/pk and this  0 as k
0 as k 
 . That is, the sequence (p, p2, p3, ...)
. That is, the sequence (p, p2, p3, ...)  0.
0.
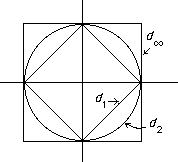 Look at the picture:
Look at the picture:
A point on the set d1 = 1 is inside the set d2 = 1 and so d2  d1 . Similarly (since the circle is inside the square) we have d
d1 . Similarly (since the circle is inside the square) we have d
 d2 .
d2 .
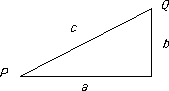 Alternatively, look at a different picture:
Alternatively, look at a different picture:
d2(P, Q) = c  a + b = d1(P, Q).
a + b = d1(P, Q).
Also, both a 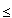 c and b
c and b 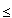 c and so
c and so
d (P, Q) = max{a, b}
(P, Q) = max{a, b} 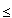 c.
c.
Without a picture, (a + b)2 = a2 + 2ab + b2 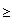 a2 + b2
a2 + b2  a + b
a + b 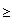
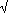 (a2 + b2) and so d1
(a2 + b2) and so d1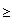 d2 .
d2 .
Also if a 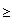 b then max{a, b} = a and since a2 + b2
b then max{a, b} = a and since a2 + b2 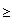 a2 we have
a2 we have 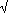 (a2 + b2)
(a2 + b2) 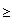 a and so d2
a and so d2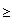 d
d .
.

If (an)  v in d1 then given
v in d1 then given  > 0,
> 0, 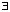 N such that n > N
N such that n > N  d1(an ,v) <
d1(an ,v) < 
 (since d1
(since d1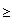 d2 and d
d2 and d ) and so convergence also takes place in d2 and d
) and so convergence also takes place in d2 and d .
.
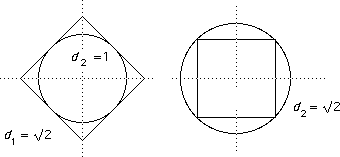 One can draw pictures to show that d1
One can draw pictures to show that d1 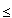
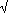 2 d2 and d2
2 d2 and d2 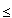
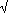 2 d
2 d .
.
(One can of course argue without using pictures too!)
Then if (an) 
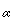 in d
in d we have:
we have:
(
 > 0) (
> 0) (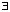 n
n  N) (
N) ( (an,
(an, 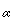 ) <
) <  )
)  d2(an,
d2(an, 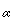 ) <
) <  /
/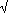 2 and d1(an,
2 and d1(an, 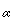 ) <
) <  /2 and so convergence also takes place in d1 and d2 .
/2 and so convergence also takes place in d1 and d2 .
Similarly, if convergence takes place in d2 it also takes place in d1 .
Combining this with the earlier result, sequences convergent in one of these norms are convergent in all of them.
 0.5 and applying f gives the sequence (0.9, 0.9, 0.99, ...)
0.5 and applying f gives the sequence (0.9, 0.9, 0.99, ...)  1 while f(0.5) = 1.
1 while f(0.5) = 1.
Hence f is not continuous and indeed is discontinuous at any terminating decimal (but continuous elsewhere).
 0.5
0.5
However, g(0.5) = 0.6111... = 11/18 which is different.