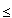Course MT4522 Metric and Topological Spaces

Solution 3

  1. |f(x) - g(x)| lte max {|f(x) - g(x)| | x belongs [a, b] = dinfinity(f, g)
    Integrate over [a, b] to get
    d1(f, g) = 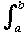intab |f(x) - g(x)| dx 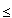lte (b - a)dinfinity(f, g).
    Hence if dinfinity(fn, f) is small, so is d1(fn, f) and so if (fn) rarrow f in dinfinity it also converges in d1 .

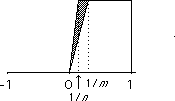  2. The graphs of fm and fn look like:

    Hence d1(fm, fn) which is the shaded region is small when m, n are large. Hence (fn) is a Cauchy sequence.


    The pointwise limit of this sequence is a function g with g(x) = 0 for x 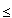lte 0 and g(x) = 1 for x > 0.
    Although (d1(fn, g) ) rarrow 0 as n rarrow infinity this function is not in C[-1, 1] and so the sequence does not have a limit in this metric space.

  3. In X every subset is open and so f -1(B) is open for all B subset Y and so f is continuous.
    If Y has the discrete metric and X does not then f will not necessarily be continuous.
    For example, the identity map from R with the usual metric to R with the discrete metric is not continuous.


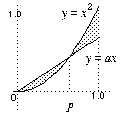    1. The line y = ax meets y = x2 where ax = x2 implies x = a at the point P
      Then d1(ax, x2) =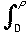 int0P (ax - x2) dx + 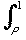intP1 (x2 - ax) dx = (eventually) 1/3 a3 - 1/2 a + 1/3 .
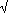      Differentiate to find where this has a minimum and get a2 = 2 implies a = 1/sqrt2 (or about 0.707)


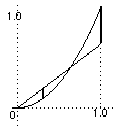    2. To find the length of the left-hand dark line differentiate d/dx(ax - x2) = 0 implies a = 2x implies x = a/2
      So the length at this point is 1/2 a2 - 1/4 a2 = 1/4 a2.
      This has to be the same as the length of the right-hand dark line which is 1 - a.
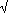      Hence we have 1/4 a2 = 1 - a implies a = sqrt8 - 2 (or about 0.828)


    3. To find the length in d2 we have
      d2(x2, ax) =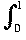 int01 (ax - x2)2 dx = (eventually) 1/3 a2 - 1/2 a + 1/5 which has its minimum (differentiate!) where 2/3 a - 1/2 = 0 implies a = 3/4 = 0.75