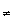 y) a 1/2 -neighbourhood of a point p is the singleton set {p}. Thus since every singleton is open and any subset A is the union of all the singleton sets of points in A we get the result that every subset is open.
y) a 1/2 -neighbourhood of a point p is the singleton set {p}. Thus since every singleton is open and any subset A is the union of all the singleton sets of points in A we get the result that every subset is open.Since all the complements are open too, every set is also closed.

Since all inverse images are open, every function from a discrete space is continuous.

If f: R
 X is continuous and X is discrete, this means that the inverse image of every singleton set is open. But then we cannot have any interval (a, b) which is mapped to more than one point. Hence the only continuous functions are constant ones.
X is continuous and X is discrete, this means that the inverse image of every singleton set is open. But then we cannot have any interval (a, b) which is mapped to more than one point. Hence the only continuous functions are constant ones.
 x2 maps (-1, 1) to [0, 1) and so open sets are not mapped to open sets necessarily.
x2 maps (-1, 1) to [0, 1) and so open sets are not mapped to open sets necessarily.
For any continuous map f: X
 Y between metric (or topological) spaces we have f -1(Y - B) = X - f -1(B). So if B is open in Y, Y - B is closed and its inverse image is the complement of the open set f -1(B) and hence is closed.
Y between metric (or topological) spaces we have f -1(Y - B) = X - f -1(B). So if B is open in Y, Y - B is closed and its inverse image is the complement of the open set f -1(B) and hence is closed.
 V
V (p). Then d(x, p) <
(p). Then d(x, p) <  and if we take
and if we take  - d(x, p) =
- d(x, p) =  a
a  -neighbourhood of x is in V
-neighbourhood of x is in V (p).
(p).If A
 X is open then A =
X is open then A =  V
V (a)(a) where the union is over all a
(a)(a) where the union is over all a  A and
A and  (a) is chosen so that V
(a) is chosen so that V (a)(a) is inside A. It is easy to verify the double inclusion to prove equality.
(a)(a) is inside A. It is easy to verify the double inclusion to prove equality.
Not every open set can be written as a union of countably many
 -neighbourhoods. For example, take R with the discrete topology. Then any
-neighbourhoods. For example, take R with the discrete topology. Then any  -neighbourhood is either R or a singleton set and so no proper uncountable set can be written as a countable union of these.
-neighbourhood is either R or a singleton set and so no proper uncountable set can be written as a countable union of these.However, R with its usual metric does have this property.
 R2 | f(x, y) > 0 } = f -1((0,
R2 | f(x, y) > 0 } = f -1((0,  )) and so is an open set.
)) and so is an open set.
For the unit disc take f(x, y) = 1 - x2 - y2
For the unit square: a function like x(1 - x) gives a vertical strip as an open set. Take the intersection of this with a similar horizontal strip.
f -1([0,
 )) is a closed set by Question 2 above.
)) is a closed set by Question 2 above.
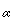
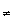
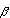 were limit points of {ai} then there would have to be subsequences converging to
were limit points of {ai} then there would have to be subsequences converging to 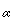 and to
and to 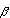 . But every subsequence of a convergent sequence converges to the same limit.
. But every subsequence of a convergent sequence converges to the same limit.
Take a union of two convergent sequences.
Take a union of countably many sequences converging to limits a finite distance apart. e.g. {m + 1/n | m, n  N}
N}
 )
) 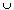 (q2 ,
(q2 ,  ) = (min{q1 , q2},
) = (min{q1 , q2},  ) and (q1 ,
) and (q1 ,  )
)  (q2 ,
(q2 ,  ) = (max{q1 , q2},
) = (max{q1 , q2},  ) and so
) and so  is closed under finite unions and intersections.
is closed under finite unions and intersections.Take a monotonic decreasing sequence of rationals (ri) converging to an irrational
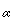 . Then
. Then 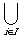 (ri,
(ri,  ) = (
) = (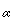 ,
,  ) and so is not in
) and so is not in  and
and  is not a topology.
is not a topology.
 is closed under finite unions and intersections. This time, however,
is closed under finite unions and intersections. This time, however,  {ni , ni+1 , ... } is in the set since the minimum min{ni | i
{ni , ni+1 , ... } is in the set since the minimum min{ni | i  N} exists since N is bounded below.
N} exists since N is bounded below.
The closed sets are the finite sets {1, 2, 3, ... , n} for each n
 N
N
The union of two countable sets is countable and since the intersection of (arbitrarily many!) countable sets is a subset of any one of them, it too is countable.
