Course MT4522 Metric and Topological Spaces

Solution 5

    1. int(Q) = empty; cl(Q) = R
    2. int(Q) = cl(Q) = Q
    3. int(Q) = empty; cl(Q) = R
    4. int(Q) = empty; cl(Q) = R
    5. int(Q) = empty; cl(Q) = Q
    6. int(Q) = empty; cl(Q) = R

    1. int(A) = empty; cl(Q) = {1, 2, ... , 48}.
    2. int(2N) = empty; cl(2N) = N

    1. Both follow from the fact that every interval contains both rational and irrational points.
    2. It is easy to verify that any infinite set is dense.

  4. The set cl(A) intersect cl(B) is a closed set which contains A intersect B and so it also contains cl(A intersect B).
    Take A = (0, 1) and B = (1, 2). Then A intersect B = empty and cl(A intersect B) = empty while cl(A) intersect cl(B) = {1}.

    If C subset D then int(C) subset int(D) (since int(C) is an open subset of D). Also int(A intersect B) subset int(A) and similarly int(A intersect B) subset int(B). Hence int(A intersect B) subset int(A) intersect int(B).
    Also int(A) intersect int(B) is an open subset of A intersect B and hence lies in int(A intersect B). Thus the two sets are equal.

    int(A) 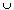union int(B) is an open subset of A 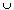union B and hence lies inside int(A 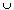union B).

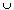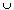    The other inclusion may fail. For example take A = [0, 1] and B = [1, 2] in R (with the usual topology). Then int(A union B) = (0, 2) while int(A) union int(B) = (0, 2) - {1}.

  5. In the usual topology finite sets are closed, but there are some closed subsets that are not finite. Thus the usual topology has more closed subsets thatn the cofinite topology and hence more open subsets. Thus it is stronger.

  6. Every singleton subset {n} is closed and hence every finite union of such sets is closed also. Hence every finite subset is closed and so every finite set is open in the subspace topology which is therefore discrete.

    In the cofinite topology on R, the subset 2Z is not closed and hence it is not closed in the subspace topology on Z. So the topology on Z is not discrete

  7. There are four topologies on X = {a, b}: discrete, trivial, {empty, X, {a}} and {empty, X, {b}}. The last two are homeomorphic.
    To handle X = {a, b, c} note that X and empty are always open and we will list the others (leaving out the { }'s and commas).
    One extra set: (3 sets in all)
    a, b, c, ab, ac, bc
    We have 6 topologies in all -- 2 up to homeomorphism.
    Two extra sets: (4 sets in all)
    a, ab (6 like this)
    a, bc (3 like this)
    We have 9 topologies in all -- 2 up to homeomorphism.
    Three extra sets: (5 sets in all)
    a, b, ab (3 like this)
    a, ab, ac (3 like this)
    We have 6 topologies in all -- 2 up to homeomorphism.
    Four extra sets: (6 sets in all)
    a, b, ab, ac (6 like this)
    We have 6 topologies in all -- 1 up to homeomorphism.
    Together with the trivial (2 sets) and discrete (8 sets) topologies, this gives the full list of 29. Up to homeomorphism there are 9 topologies.

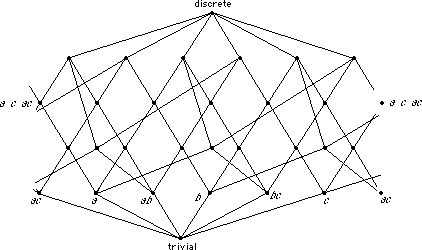
    Here is a "lattice diagram" showing how they are related.
    Topologies with the same number of sets are on the same level.
    [The {ac} and {a c ac} "points" have been plotted twice to make the diagram more symmetric.]