Solution 6

1. A subset U is closed in the subspace topology A - U is open in the subspace topology A - U = A Y for Y open in X U = A (X - Y) and X - Y is a closed subset of X.
   1. This is false. Take U = A = [0, 1] R = X. Then A is open in A and so the interior of U in the subspace topology is [0, 1] but in the usual topology on R it is (0, 1).
      
   2. This is also false. Take U = A = (0, 1) R = X and argue similarly.
      
   
   

2. To prove that ₁ and ₂ are topologies it is easiest to work with closed sets.
   In ₁ proper closed sets are finite and this set is easily seen to be closed (!) under arbitrary unions and finite intersections.

   In ₂ proper closed sets are either finite or contain 1. Again it is easily seen to be closed under arbitrary unions and finite intersections.

   ₂ is stronger (more open sets) than ₁ and so the identity map from (X, ₂) to (X, ₁) is continuous but its inverse is not.

   Consider the map g: (X, ₁) (X, ₂). The set B = N - {1} is open in ₂ but g^-1(B) = 2N and is not open in ₁ . Hence this map is not continuous.

   Consider the map g: (X, ₂) (X, ₁). Take U ₁ . Then N - U is finite.
   If 1 U then since g(1) = 1, we have 1 g^-1(U) and so g^-1(U) is open.
   If 1 U then N - g^-1(U) contains only finitely many even integers and so g^-1(U) is an open subset.
   Hence g is continuous.

3. 1. We prove these sets equal by proving a double inclusion.
      So suppose (x, y) cl(A) cl(B). Let W be an open set containing (x, y) in cl(A) cl(B). Then W contains a subset of the form U V with x U and U open in X and y V and V open in Y since sets of this form are a basis for the topology. But U meets A (since x cl(A) ) and V meets B. So U V and hence W meet A B. Hence (x, y) cl(A B).

      To prove the other inclusion, suppose now that (x, y) cl(A B). Then every open set containing (x, y) of the form U V meets A B. Hence every open set U containing x meets A and every open set V containing y meets B. Thus x cl(A) and y cl(B) and so (x, y) cl(A) cl(B).

   2. One may use a similar double inclusion or use the fact (Exercise!) that int(A) = X - cl(X - A).
      

4. If an open set A is a union (over i) of intersections (over j) of sets U_i,j of sets of the subbasis then f ^-1(A) is the corresponding union of intersections of the f ^-1(U_i,j) and providing all these are open the union of the (finite) intersections of them will be too.

   An interval (a, b) = (-, b) (a, ) and since the intervals form a basis, the unbouded ones form a subbasis. However, taking unions of such intevals never gives a bounded set and so they do not form a basis.
   
   U (V = U Y) (X V) and so every set in the basis can be written as such an intersection.

5. Any open interval (a, b) in R can be written as a union of -neighbourhoods of rational points with rational by taking ssuitable rational sequences converging to a (from above) and b (from below). Since these intervals form a basis the rational neighbourhoods do too. There are only countably many of these.
   Every basis for the discrete topology must contain all the "singleton" sets and so is uncountable.

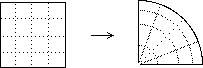6. The map acts like :
   It is easy to see that this is a bijection. (It would not be if we took the closed square and quadrant.)

   To see that it is a homeomorphism take small open sets in each space and see what their images are.
   
   
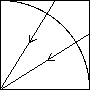   To see that the closed square and quadrant are homeomorphic, take a different map which "shrinks back" along the radius as shown.
   
   
   

7. The space [0, 1) (0, 1) is the set: (including the left-hand edge) while [0, 1) [0, 1] is: (including the edges marked).

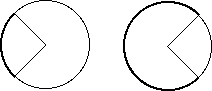   To see that these are the same use a homeomorphism to map the squares to discs and then "expand the sector" to get a homeomorphism.