Solution 7

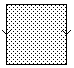
1. In both cases the space is:
   and we get a one-one correspondence by mapping the points to the corresponding points on the square.

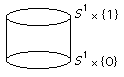2. We start with a cylinder:
   
   
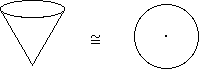   Identifying the "bottom ring" to a point gives a cone:
   which is homeomorphic to a disc.
   
   
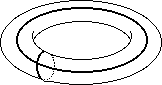
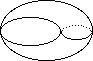   Identifying both top and bottom to a single point gives a space like:
   
   
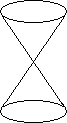   Identifying a "middle ring" to a single point gives a kind of "double cone":
   
   
   

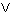3. Every point of X Y is either a point of X or a point of Y -- except for x X, y Y which map to the same point of X Y/~.
   So we may map points in X - {x} to X {y} in X Y, points in Y - {y} to {x} Y in X Y and map the common point to (x, y) X Y and verify that this is a homeomorphism.

   To get S¹ S¹ start by identifying the top and bottom of the cylinder (see Question 2 above) to get a torus S¹ S¹.
   Then S¹ 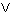S¹ is a pair of circles.
   
   
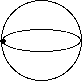   Shrinking one of them down to a point gives the space in the last part of Question 2. Then shrink the second circle down to the point to get a sphere.
   
   
   

4. This is the construction of the additive quotient group R/Q. Any real number x R can be written as n + f with n Z and f (0, 1). So the interval (0, 1) maps to the whole of R/~.
   Similarly for any other open interval.
   The open sets of the identification topology are the images of open sets in R. Since any non-empty open set of R contains an open interval, it will map to the whole of R/~. Hence R/~ (which is an uncountable set and hence can be put into one-one correspondence with R) has only itself and as open sets.
   Thus, up to homeomorphism, it is the same as R with the trivial topology.

5. Note that the boundary of A is a pair of circles -- linked non-trivially. Thus A is the same as a "twisted cylinder" (Question 1 above)
   Reversing the twist on one of the strips gives a surface with two unlinked circles as boundary. This is an ordinary cylinder in R³.

   The space B is trickier. Its boundary is a single circle in R³ which happens to be knotted.
   Unlikely as it may seem, B is a torus with a disc removed to make a hole.
   To see this, snip two of the twisted strips: 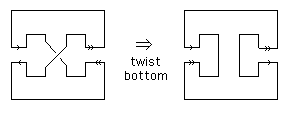and convince yourself that this is the same as a torus with a hole:
   
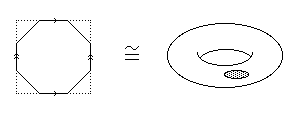
   Reversing a twist makes no difference (think how the identifications are made) while if one of the strips is untwisted A is a Mobius band and B is a cylinder with a hole.