Solution 1

1. If Achilles catches the tortoise after t seconds, then the distance he runs is:
   10 t = 100 +10t/17 ⇒ 16t/17 = 10 ⇒ t = 170/16 or 10 ⁵/₈ seconds.

   Generating the Geometric series gives:
   10 + 10/17 +10/17² + 10/17³ + ... and [recalling that the sum of a + ar + ar² + ar³ + ... = a/(1 - r)] this sum is 10/(1 - ¹/₁₇) which is the same.

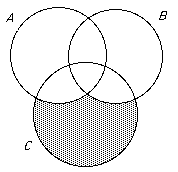2. (a) Look at the Venn diagram:

   Both sides of the identity are the shaded area.

   (b) Take D to be the empty set and it is easy to see that the statement is then false.

   (c) If (x, y) ∈ LHS then x ∈ A ∪ B and y ∈ A ∪ C and so (x ∈ A or x ∈ B) and (y ∈ A or y ∈ C). Looking at these four possibilities gives (x, y) ∈ A × A or (x, y) ∈ A × C or (x, y) ∈ B × A or (x, y) ∈ B × C and so LHS ⊆ RHS.
   The proof that RHS ⊆ LHS is similar.
   
   
   

3. The first statement is true since one can take y = x.
   The second statement is false since there is no choice of y which will work for all x.
   In the third statement we may take y = 0 and this choice will work for all values of z and so the statement is true.
   If the statement ¬(∀x)P is true then (∀x)P is false and so there must be some x for which P is false. That is (∃x)(¬P).
   Similarly, if ¬(∀x)P is false then (∀x)P is true and so there is no x for which ¬P is true. That is (∃x)(¬P) is false.

4. If x + r = s were rational then x = s - r would be rational and this gives a contradiction.
   The proof that x - r and xr are irrational is similar.
   
   The number x + y is not necessarily irrational. For example, x = -y = √2 gives a counterexample.
   Similarly, taking x = y = √2 shows that x - y, xy and x/y may be rational. Of course, these combinations may be irrational for some values of x, y.
   
   Take the point which divides the interval (r, s) in the ratio of 1 : √2. This is (√2 r + s)/(√2 + 1) and lies between r and s. It is a simple exercise to verify that if this were rational then √2 would be also.

5. If √n = a/b (with a/b in lowest terms) then a²/b² = n and so b² divides a². If a and b >0 and have no common factors, this is impossible.
   
   If √(n + 4) + √(n - 4) is rational, then its square is rational ⇒ n + 4 +2√(n + 4)√(n - 4) + n - 4 is rational ⇒ √(n² - 16) is rational ⇒ (from the last result) n² - 16 = m² for some integer m. Then (n - m)(n + m) =16 and there are only a few possibilities ⇒ n = 5, m = 3 and putting n = 5 in the original expression gives a solution.
   
   Solutions of the quadratic are -b √(b² - 2) and so are rational ⇔ b² - 2 = d² for d rational. Then (b - d)(b + d) = 2 and this has no integer solutions.

6. Suppose √3 = a/b. Then 3b² = a² and so a is divisible by 3. Then the RHS is divisible by 9 and so b² is divisible by 3 and b is divisible by 3. Thus a, b have a common factor and we could have assumed that a/b was in "Lowest terms" and get a contradiction.
   
   A similar proof (using divisibility by either 2 or 3) shows that √6 is irrational.
   
   If √2 + √3 were rational, then its square: 2 + 2√6 + 3 would be also, from which one could deduce that √6 is rational.
   
   If √m + √n = r is rational then r²= M + n + 2√mn and so √mn = s would be rational.
   Then n = s²/m and r² = m + s²/m + 2s = (s+m)²/m. Hence m = (s+m)²/r² = [(s+m)/r]² and so √m would be rational.
   
   

7. With P on one side and Q on the other, if P were true then Q would be true ⇒ P would be false.
   If P were false then Q would be false ⇒ P would be true. So in either case we get an inconsistent system.
   
   If P were on both sides of the card then P can be either true or false and we get no contradiction.
   
   With Q on both sides, Q false ⇒ Q true and vice versa and we get an inconsistent system