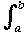Solution 10

1. |f (x) - g(x)| ≤ d_∞(f, g) for x ∈ [a, b]. So |f (x) - g(x)| dx ≤ 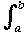d_∞(f, g) dx = (b - a)d_∞(f, g).
   So if we have d_∞(f_n, f) < ε for large n, we have d₁(f_n, f) ≤ (b - a)ε which is small for n large and so (f_n)→ f in d₁ also.
   In fact if (f_n)→ f in d_∞ it also converges in d₂ though the inequality is a bit trickier.

2. h(0) = f (0) - f (¹/₂) and h(¹/₂) = f (¹/₂) - f (1) = f (¹/₂) - f (0) and so h changes sign on [0, ¹/₂] and so has a zero here.
   
   
   Measure distance around the equator and scale it to fit into [0, 1]. Note that 0 and 1 represent the same point. Then assuming that temperature varies continuously, you can use the last result to deduce that two opposite points have the same temperature.

3. Take δ = ε in the definition to see that a function satisfying the given condition is continuous.
   Assume that m < n and put |a₁ - a₂| = R. Then |a₂ - a₃| = |f (a₁) - f (a₂₎| ≤ λR, and so on.
   In general |a_m - a_m+1| ≤ λ^m-1R and |a_m - a_n| ≤ (λ^m-1 + λ^m + ... + λⁿ)R.
   Since the Geometric series 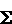λⁿ is convergent, its partial sums form a Cauchy sequence and so the above expression can be made as small as we like by choosing m, n large. Thus (a_n) is a Cauchy sequence and hence has a limit α. By the usual argument α satisfies the equation f (α) = α and so is a fixed point for f.
   
   If β is another fixed point then f (α) - f (β) = α - β and since we have |f (α) - f (β)| < 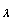|α - β| this is impossible unless α = β. Thus the fixed point is unique.

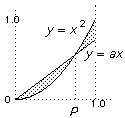4. The line y = ax meets y = x² where ax = x² ⇒ at P we have x = a.
   Then d₁(ax, x²) = 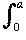(ax - x²) dx + 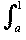(x² - ax) dx = [ax²/₂ - x³/₃ 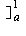+ [x³/₃ - ax²/₂ 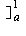= a³/₃ - a/₂ + ¹/₃.
   Differentiate to find the minimum of this.
   This occurs when a² - ¹/₂= 0 or at a = 1/√2 = 0.707 (approximately).

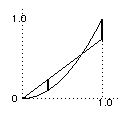5. To find the length of the "Left-hand thick line" where the distance between the graphs is a maximum, differentiate: ^d/_dx(ax - x²) = 0 ⇒ a = 2x ⇒ x = a/₂.
   So the length of the "Left-hand thick line" a²/₂ - a²/₄ = a²/₄.
   The length of the "right-hand thick line" is 1 - a and so if these two lengths are the same we have a²/₄ = 1 - a ⇒ a = √8 - 2 = 0.828 (approximately).

6. To find the distance between the two curves in the metric d₂ we have:
   [d₂(x², ax)]² = 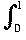(x² - ax)² dx = [x⁵/₅ - ax⁴/₂ + a²x³/₃ 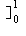= a²/₃ - a/₂ + ¹/₅
   and we can differentiate to find where this is a minimum ⇒ 2a/₃ - ¹/₂ = 0 ⇒ a = ³/₄ = 0.75