Solution 2

1. (a) not one-one, not onto
   (b) one-one correspondence
   (c) one-one, not onto
   (d) one-one, not onto
   (e) one-one correspondence
   (f) one-one, not onto
   (g) Draw the graph to see that it is not one-one but is onto
   (h) not one-one, not onto

2. (a) Let x ∈ f[A ∩ B]. Then x = f (y) for y ∈ A ∩ B. So y ∈ A and x ∈ f[A]. Similarly x ∈ f[B] and so x ∈ f[A] ∩ f[B].
   
   Suppose f is one-one and let y ∈ f[A] ∩ f[B]. Then y = f (a) for a ∈ A and y = f (b) for b ∈ B. Thus f (a) = f (b) and by the one-one property, a = b A ∩ B. Hence y ∈ f[A ∩ B] and the two sets are equal.
   
   
   (b) Let x ∈ f[f ^-1[B]]. Then x = f (y) for y ∈f ^-1[B]. Hence f (y) ∈ B and we have f[f ^-1[B]] ⊆ f[B].
   
   If f is onto, take y ∈ f[B]. Then y = f (b) for some b ∈ B. By the onto condition, b = f (a) for some a ∈ f ^-1[B] ⊆ X. Thus y ∈ f[f ^-1[B]] and the two sets are equal.
   
   

3. Each element of A may be mapped to any element of B and so we get n^m different maps.
   If the map is one-one we have a choice of n elements for the image of the first element of A, a choice of n - 1 for the second, etc. Thus we have n(n - 1)(n - 2) ... (n - m +1) = ^n!/_m! one-one maps. (Of course, if m > n we get no such maps.)

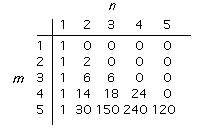   The number of onto maps is harder to calculate.
   
   The number of onto maps from a set of size m to a set of size n are shown on the right for some small values.

   These numbers are related to numbers discovered by the Scottish mathematician James Stirling (1692 to 1770).
   
   

   If f: A→ B is a one-one map defined on a finite set A then the image of f has the same number of elements. Hence if |A| =|B| the map is onto. Example 1f) above shows that this result may fail for infinite sets.

4. The function which maps (m, n) to 2^m3ⁿ is one-one by the uniqueness of factorisation. This maps N × N onto its image is a one-one correspondence. This image is a subset of N and hence is countable.
   Define a map from N × N × ... × N→ N by mapping (a₁ , a₂ , ... , a_n) to p₁^a₁p₂^a₂ ... p_n^a_n where p₁ , ... , p_n are distinct primes and the result follows in a similar way.

5. Choosing a subset of a set with n elements means making a choice about whether to include each element or not, so you get a choice of 2ⁿ possible subsets.
   [Equivalently, a map from a set S to {0, 1} corresponds to a subset by mapping the elements of the subset to 1 and the other elements to 0. (This is called the characteristic function of the subset.) By question 3 above, there are 2ⁿ such maps.]

   Hence the set of all finite subsets is ∪{subsets of size n} where the union is taken over all n ∈ N. This is a countable union of finite sets and hence is countable.
   
   We can adapt the Cantor diagonalisation process as follows.
   Suppose A₁, A₂ , A₃ , ... is a counting of all the proper (≠ N) subsets of N.
   Let X be the set {a₁ , a₂ , a₃ , ...} where a₁∉ A₁ , a₂∉ A₂ , ...
   Then the set X is not in the counting.

6. Tabulating f as suggested gives a table as on the right:

   This gives a one-one correspondence between N × N and N which is similar to (but not quite the same as) that given in the section on Infinity and infinities.
   (One starts at the bottom of the line m + n = constant each time.)