Solution 6

1. (a) a_n - a_n-1 = (n + 1)/(n + 2) - n/(n + 1) = 1/[(n + 1)(n + 2)] > 0. Hence the sequence is monotonic increasing.
   (b) a_n - a_n-1 = n + 1 + 8/(n + 1) - n - 8/n = 1 - 8/[n(n + 1)] and so this is positive provided n ≥ 3 and the sequence is monotonic increasing from then on.
   (c) The sequence is (0, 3, 2, 5, 4, 7, 6, ... ) and never becomes monotone.
   (d) The sequence is (1, 5, 5, 9, 9, 13, 13, ... ) and is monotone.

2. s_n+1- s_n= 1/(n+1)²> 0 and so the sequence is monotonic increasing.
   Clearly s₁≤ 2 - 1/1. Now assume the result is true for n = k and consider s_k+1= s_k+ 1/(k + 1)²≤ 2 - 1/k + 1/(k + 1)² (by the inductive hypothesis) and this can be written as: 2 - 1/(k + 1) × [(k + 1)/k - 1/(k + 1)] = 2 - 1/(k + 1) × [(k² + k + 1)/(k² + k)] ≤ 2 - 1/(k + 1) as required.
   So the sequence of partial sums is monotonic increasing and bounded above and hence convergent.

   Proving that its sum is π²/6 is quite a bit harder. One can do it by defining a function f (x) = 0 if -π ≤ x ≤ 0 and x² if 0 < x ≤ π and expanding it as a Fourier series, though that is not how Euler originally proved it!

3. a_nis the partial sum of the (divergent) harmonic series: 1 + ¹/₂ + ¹/₃ + ¹/₄ + ... . Hence (a_n) is not a Cauchy sequence even though |a_n+1 - a_n|→ 0 as n→ ∞.

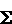4. Since s_n+1 - s_n = b_n+1 ≥ 0 the sequence (s_n) is monotonic increasing. It is bounded above by the limit of c_n and hence is convergent.

5. Assume m > n and we will prove that |a_n - a_m| is small for large enough m, n.
   |a_n - a_m| = |a_n - a_n+1 + a_n+1 - a_n+2 + ... + a_m-1 - a_m| ≤ |a_n - a_n+1| + |a_n+1 - a_n+2| + ... + |a_m-1 - a_m| ≤ rⁿ + rⁿ⁺¹ + ... + r^m. Since this is part of "the tail" of the convergent Geometric Series: 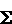rⁿ this is small for large m, n.
   The sequence (a_n) is certainly bounded above by 1. Now a_n+1 - a_n = a_n/3 + 2a_n-1/3 - a_n and so |a_n+1 - a_n| = ²/₃|a_n - a_n-1|. Now use induction to get |a_n+1 - a_n| ≤ (²/₃)ⁿ and then the last result shows that we have a convergent sequence.

   Finding its limit is rather tricky. Experimenting with Maple suggests that ³/₅ is a good guess.
   A standard way of dealing with recurrence relations like this one is to guess a solution of the form a_n = μⁿ which in this case gives μ = 1 or -²/₃ and the general solution is then of the form a_n= A.1ⁿ + B.(-²/₃)ⁿ for some constants A and B.
   Choosing A and B to give the correct answer for a₁ and a₂ gives the formula a_n = ³/₅ + ⁹/₁₀ × (-²/₃)ⁿand so as n→ ∞ we have (a_n)→ ³/₅.

6. Your calculator should convince you that as x→ 0+, x^x→ 1. (For example, for x = 0.001, x^x= 0.993... )
   To prove it, take logarithms. (The log function treats limits nicely since it is a continuous function for x > 0.)
   log(x^x) = x log(x) = log(x)/(¹/_x) and then by l'Hôpital's rule this limit is (¹/_x)/(^-1/_x²) = -x→ 0 as x→ 0.
   Hence the limit of x^x as x→ 0 is e⁰ = 1.
   For the last part, put x = ¹/_n.

7. Let x_n = (1 + R/n)ⁿ where R is the rate of interest. Then if the limit of the sequence (x_n) = α, by the continuity of the logarithm function we have the limit of the sequence (log(x_n)) = log(α).
   Now log(x_n) = n log(1 + R/n) and by l'Hôpital's Rule, if x = ¹/_n, the limit of 1/x × log(1 + Rx) as x→ 0+ is the same as the limit of R/(1 + Rx) which is R. Hence the limit of the sequence (x_n) is e^R. If R = 0.12 this is about 1.127. So after a year you have N × 1.127 -- slightly more than the N × 1.12 you would have had with simple interest.