Solution 7

1. (i) Take the sequence (x_n) = (¹/_n)→ 0. Then f (¹/_n) = 1. So, applying f to the sequence (x_n) gives the constant sequence converging to 1 ≠ f (0). Hence f is not continuous at 0.

   (ii) Take ε = ¹/₂. Then any interval (-δ, δ) containing 0 contains points where f (x) = 1 and so we cannot have |f (x) - f (0)| < ε for all the points in such an interval.

2. Note that the proof that the function f (x) = x² is easy using the sequential definition.
   Using the ε-δ definition: given ε > 0 we need to find δ such that |x - 1| < δ ⇒ |x²- 1| < ε.
   But |x²- 1| = |x - 1||x + 1| and so provided that x < 2, this is < |x - 1|/3. So taking δ < max{1, ε/₃} will do.

3. 
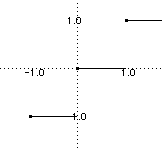
   The graph of the floor function is:
   To show this is discontinuous at any k ∈ Z, look at a sequence (k - ¹/_n) approximating k from above and argue as in Question 1.
   To see that it is continuous at any other point, use the fact that if x is not an integer, then the nearest integer is at least δ away from x for some 0 ≤ δ ≤ ¹/₂. Then on the interval (x - δ, x + δ) the function is constant and hence continuous.
   
   

   
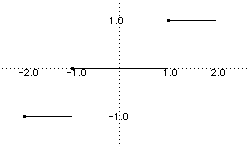
   The [x] function (though be careful, because different references are by no means consistent!) is "x rounded towards zero and so has a graph:

   The proof is similar to that above.
   
   

   The fractional part {x} can be written as {x} = x - [x] and so has the same points of discontinuity as [x].

4. If p > 0 then we can choose a δ so that on the interval (p - δ, p + δ) we have h(x) = g(x) and so h is continuous since g is. Similarly if p < 0.
   Finally at p = 0, given ε > 0, we can find δ such that |f (x) - f (0)| < ε and |g(x) - g(0)| < ε in the interval (-δ, δ). Then we have |h(x) - h(0)| < ε on this interval and so h is continuous.
   
   The function |x| is made by putting together the functions f (x) = x and g(x) = -x and so is continuous by the last result.
   
   The function |f (x)| is the composite of the function f and x ↦ f (x) and so is continuous.
   
   The function M(x) = ¹/₂[(f (x) + g(x)) + |f (x) - g(x)|] and so is made from continuous functions using arithmeticc operations and the x ↦ |x| function. Hence it is continuous.
   Similarly m(x) = ¹/₂[(f (x) + g(x)) - |f (x) - g(x)|] is continuous.

5. 
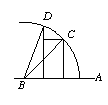
   Note that the angles are measured in radians so that |x - y| is the length of the arc CD.

   |sin (x) - sin(y)| is the length of the line DE and so the result follows for x, y < π/2. A little thought shows that the result still holds if x, y are in different quadrants.
   
   Then using the ε-δ definition of continuity, we can take δ = ε and verify continuity at any point.
   
   For the cosine function, either argue as above with |cos(x) - cos(y)| = the length of EC or (easier!) use cos(x) = sin(π/2 - x) and compose continuous functions.
   
   The function tan(x) = sin(x)/cos(x) is then continuous wherever cos(x) ≠ 0. That is for x ≠ (k + ¹/₂)π for k ∈ Z.