Solution 8

1. 
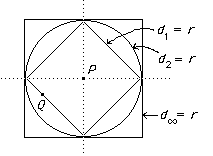
   Look at the picture:

   If a point Q is as shown, it is clear that d₂(P, Q) ≤ r since "The diamond is inside the circle" and so d₂(p, Q) ≤ d₁(p, Q).
   Similarly, "The circle is inside the square and so d_∞(P, Q) ≤ d₂(P, Q).
   
   
   
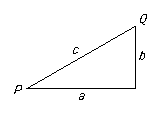
   Alternatively, look at the picture:

   Then d₂(P, Q) = c ≥ a + b = d₁(P, Q).
   Also both a≤ c and b ≤ c ⇒ d_∞(P, Q) = max{a, b} ≤ c.
   
   
   Without a picture, one can argue
   (a + b)² = a² + b² + 2ab ≥ a² + b² ⇒ a + b ≥ √(a² + b²) ⇒ d₁≥ d₂.
   Also, if a ≥ b then max{a, b} = a and since a²+ b²≥ a²we have √(a² + b²) ≥ a and so d₂ ≥ d_∞.
   
   If (a_n)→ α in d₁, then given ε > 0 ∃ N such that n > N ⇒ d₁(a_n, α) < ε ⇒ (since d₁≥ d₂and d_∞) that the sequence converges in d₂ and d_∞ also.

   
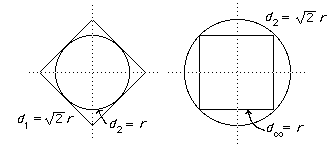
   One can draw the pictures :

   to show that d₁≤ √2 d₂ and d₂≤ √2 d_∞.
   
   
   Alternatively, √2 √(a² + b²) ≥ a + b ⇔ 2(a² + b²) ≥ a² + 2ab + b² ⇔ a² + 2ab + b² ≥ 0 which is true since (a - b)² ≥ 0. Hence √2 d₂ ≥ d₁.
   
   If (a_n)→ α in d_∞, then given ε > 0 ∃ N such that n > N ⇒ d_∞(a_n, α) < ε ⇒ d₂(a_n, α) < ε/_√2 and d₂(a_n, α) < ε/₂ and so the sequence converges in d₁ and d₂ also.

   Similarly, if convergence takes place in d₂ it also takes place in d₁. Combining this with the earlier result shows that sequences which converge in one of these metrics converge in them all.

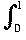2. d₁(f_n, 0) = nxⁿ- nxⁿ⁺¹dx = [n/(n + 1) xⁿ⁺¹ - n/(n + 2) xⁿ⁺² 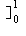= n/[(n + 1)(n + 2)]→ 0 as n→ ∞.
   Thus (f_n)→ the 0-function.
   To find the maximum, solve ^d/_dxf_n(x)= 0 to get:
   n²x^n-1 - n(n+1)xⁿ = 0 ⇒ x = n/(n + 1) or 0.
   The maximum is at n/(n + 1) and is thus [n/(n + 1)]ⁿ = [1 - 1/(n + !)]ⁿ⁺¹→ e^-1as n→ ∞ (by Exercises 6 Question 7).
   Thus d_∞(f_n, 0) does not converge to 0 in R as n→ ∞ and so (f_n) does not converge to the 0-function in d_∞.

3. (a)  The sequence (0.49, 0.499, 0.4999, ... )→ 0.5 and applying f gives (0.9, 0.9, 0.99, 0.99, ... )→ 1.0 while f(0.5) = 0. Hence f is not continuous at 0.5. In fact, a similar proof shows that f is not continuous at any terminating decimal -- though it is continuous at all other points.

   (b)  Apply g to the same sequence to give (0.50111... , 0.500111... , 0.5000111... , ... ) which converges to 0.5. However, g(0.5) = 0.6111... which is different and so g is discontinuous at 0.5.

   (c)  This map is actually the map h(x) = 1 - x as you can see most easily by writing 1 as 0.9999... . Hence it is continuous everywhere.