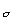Solution 9.2

Let _n be the partial sum of 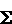f_i, assume that m > n and look at d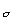_∞(_m- 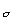_n) = max { |f_n+1(x) + ... + f_m(x)| for x ∈ [a, b]} ≤ max {|f_n+1(x)| + ... + |f_m(x)| } ≤ M_n+1+ ... + M_m.
Since the series 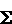M_i converges, its partial sums form a Cauchy sequence and so M_n+1+ ... + M_m is small for large m, n. Thus (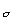_n) is a Cauchy sequence in C[a, b] and since this is a complete space under d_∞ the sequence is convergent to its pointwise limit and this limit is continuous.

Since |sin²(x)| ≤ 1, we may take M_n= 1/n² and so by the Weierstrass M-test, the series 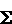sin²(x)/n² is uniformly convergent to a continuous function.
Deciding exactly where this function is differentiable is much harder.

Similarly, since |cos(aⁿx)| ≤ 1, if 0 < b < 1 we may take M_n= 1/bⁿ and use the fact that 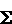M_n is convergent to deduce that Weierstrass's function is continuous.
Proving that this function is not differentiable anywhere is the hard bit!