If a, b are real numbers then | a + b | ≤ | a | + | b |.
When is this inequality strict ?
Why is it called the Triangle inequality ?
Use induction to prove that if a1, a2, ..., anare any real numbers then |
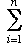 ai| ≤
ai| ≤ 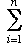 |ai|.
|ai|.
If an≤ xn≤ bn for all n and the sequences (an) and (bn) converge to the same limit, then (xn) also converges to this limit.
(a) convergent but not monotonic,
(b) bounded but not convergent,
(c) convergent but not bounded,
(d) monotonic but not bounded,
(e) divergent to +∞ but not monotonic,
(f) monotonic and bounded but not convergent,
(g) unbounded but not monotonic,
(h) positive and convergent, but not monotonic.
Do the same thing for the sequence ( (2n2+ 1)/(n2+1) ).
(a) (|an|) converges but (an) does not converge,
(b) (an) converges but (|an|) does not converge,
(c) (an) and (bn) do not converge, but (an+ bn) converges,
(d) (an) and (an+ bn) converge but (bn) does not converge.
For example, if a = 0.1234567... then a1 = 0.234567.., a2 = 0.34567..., etc.
For which a is the sequence (an) convergent and what is its limit ?