Some theorems in plane projective geometry

We may prove theorems in two-dimensional projective geometry by using the freedom to project certain points in a diagram to, for example, points at infinity and then using ordinary Euclidean geometry to deal with the simplified picture we get.

1. The harmonic property of the complete quadrangle/quadrilateral.

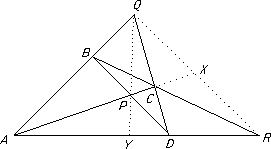
   A complete quadrangle ABCD is a set of 4 vertices together with the set of 6 lines joining them.
   These define the three diagonal points PQR.

   The cross ratio (A, C ; P , X) = -1
   
   
   Proof
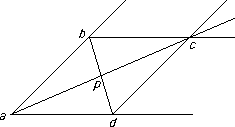   Project te points Q and R to points at infinity. This gives the diagram on the right in which abcd is a parallelogram and so ap = pc.
   Thus, since x is at infinity also, (a , c ; p, x) = -1 and the result follows.
   
   
   Remark

   The range (A, Y, D, R) is also harmonic. This gives a method of constructing such harmonic ranges and is the starting point for a variety of geometric constructions.

2. Desargues theorem
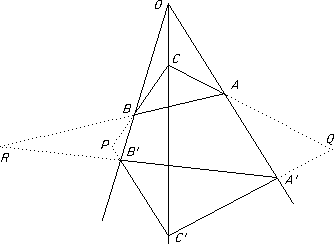   (First proved by Girard Desargues (1591 to 1661) In 1639)
   Two triangles in perspective from a point have corresponding sides meeting in a line.

   That is, in the diagram shown in which the lines AA', BB', CC are concurrent in a point P, the meets of AB and A'B', of AC and A'C' and of CB and C'B' are collinear.
   
   
   Proof
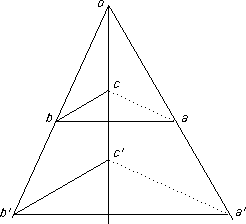   Project the points P and R to infinity to get the diagram shown.
   By similar triangles, ac is parallel to a'c' and so e too is on the line at infinity and so p, q, r are collinear and so too are P, Q, R.
   
   
   Remarks

   1. One my also prove this result in 3-dimensional space by observing that the line PQR is the meet of the planes ABC and A'B'C'. The two dimensional case then follows by projection of this 3D figure into a plane.

   2. This result fails in some projective planes (over finite fields).