That is, in homogeneous coordinates:
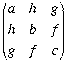 and x =
and x = 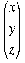 .
.This however includes some singular conics like:
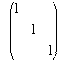 or x2 + y2 + z2 = 0 ⇒ empty set
or x2 + y2 + z2 = 0 ⇒ empty set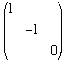 or x2 - y2 = 0 ⇒ two lines x = y and x = -y
or x2 - y2 = 0 ⇒ two lines x = y and x = -y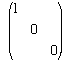 or x2 = 0 ⇒ one line x = 0
or x2 = 0 ⇒ one line x = 0
| Previous page (Duality) | Contents | Next page (Elliptic geometry) |
As we saw earlier, a conic section is the intersection of a (double-ended) right circular cone with a plane.
Remarks
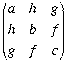 and x =
and x = 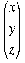 .
.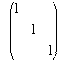 or x2 + y2 + z2 = 0 ⇒ empty set
or x2 + y2 + z2 = 0 ⇒ empty set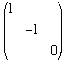 or x2 - y2 = 0 ⇒ two lines x = y and x = -y
or x2 - y2 = 0 ⇒ two lines x = y and x = -y or x2 = 0 ⇒ one line x = 0
or x2 = 0 ⇒ one line x = 0
Here is a result proved by the French mathematician Michel Chasles (1793 to 1880) in 1852.
Chasles' theorem
Let A, B, C, D be distinct points on a (non-singular) conic. If P is another point on the conic then the cross-ratio of the pencil PA, PB, PC, PD does not depend on the point P
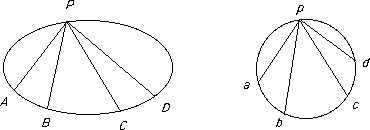 Proof
Proof
By Exercises 8 Question 4, the cross-ratio of a pencil is the cross-ratio of the four points at which the pencil meets any line.
Project the conic into a circle. The cross ratio of the pencil is determined by the angles beween the lines PA, PB, PC, PD and if we move the point on the circle these angles are unchanged.

Remark
From this last result, if four points lie on a conic we may unambiguously talk about their cross-ratio.
We can now prove a result discovered by the French mathematician Blaise Pascal (1623 to 1662) when he was 16 years old. He called it the mysterium hexagrammicum = mystic hexagram.
Pascal's theorem
If a hexagon is inscribed in a (non-singular) conic then the meets of opposite sides are collinear.
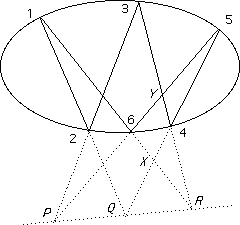 Proof
Proof
Project from 1: (2 , 4 ; 5 , 6) = (Q , 4 ; 5 , X)
Project from 3: (2 , 4 ; 5 , 6) = (P , Y ; 5 , 6)
Now consider the two pencils with vertex R and we get
(RQ , R4 ; R5 , RX) = (RP , RY ; R5 , R6)
But R6 = RX, R4 = RY and so RP = RQ and P, Q, R are collinear.

Remarks
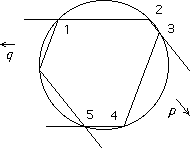
Brianchon's theorem
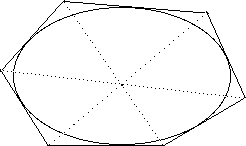 If a hexagon is circumscribed to a conic then the joins of opposite points of the hexagon are concurrent.
If a hexagon is circumscribed to a conic then the joins of opposite points of the hexagon are concurrent.
| Previous page (Duality) | Contents | Next page (Elliptic geometry) |