Course MT3818 Topics in Geometry

Solutions 2

  1. The proof is similar to the proof that SO(3) is the group of rotations in R3.
    An element T of O(3) as an eigenvalue which is either ±1. If λ = +1 then T has a fixed vector a and acts like an element of O(2) in the plane perpendicular to a.
    If it acts as a rotation here, then we have a rotation in R3. (case (a))
    If it acts as a reflection in a vector b here, then we have a reflection in the plane containing a and b. (case (b))
    If T has no positive eigenvalue then as above we have λ = -1 with eigenvector c . As before T acts as an element of O(2) in the plane perpendicular to c and it cannot act as a reflection here otherwise it would have a fixed vector (which would be an eigenvector of +1). Hence it acts as a rotation in this plane and we have case (c).


    i) The product of two reflections (which have determinant -1) has determinant +1 and so is a rotation. Since the vector b is fixed, it is a rotation about b.

    ii) This is case (c): rotation by π about the z-axis followed by reflection in the (x, y)-plane.

    iii) Products of rotations are always rotations since SO(3) is a subgroup and so we have case (b).
    Seeing what the axis is can be rather tricky. For example, rotation (by π/2 anticlockwise) about the x-axis, followed by rotation about the y-axis followed by rotation about the z-axis is rotation by π/2 about the y-axis.

  2. A rotation by θ can be written as a reflection in the x-axis followed by a reflection in a line making an angle of θ/2 with the x-axis as you can see by looking at the result of acting on the standard basis. In fact, reflections in any pair of lines at an angle of θ/2 will give the same result.


    In the last question we showed that an element of O(3) is either a reflection , a rotation by θ about some axis a (in which case it can be written as a production of two reflections in planes meeting in a at an angle of θ/2) or a rotatory reflection (in which it can be as the product of three reflections).


  3. If f = Ta ∘ L then f(0) = Ta ∘ L(0) = a and hence a is uniquely determined. Thus L = T-a ∘ f is also determined.


    If f(x) = L' ∘ Tb(x) then apply the transformation to f -1(0) to get 0 = L'(b + f -1(0)) and so we can take b to be -f -1(0) and then solve to find the linear map L' = f ∘ T-b.

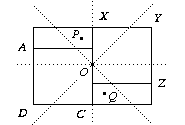  4. There is a choice of four positions for A to go to and then two possibilities for B. So there are eight symmetries in all.
    These are: translation by a vector parallel to AX, rotations by π about O and by π/2 about the points P, Q and four glide reflections along the dotted lines.

    You can see this a different way by observing that the symmetries mapping one square to the other can be obtained by composing (say) the translation by the symmetries that map the second square to itself. That is TAX∘D4, where the dihedral group acts fixing the centre of XYZT.

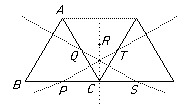  5. Either argue as in the last question or observe that an equilateral triangle has 6 symmetries to deduce that there are 6 symmetries mapping one triangle to the other.
    These 6 can be thought of (for example) as the compositions of a horizontal translation and a self symmetry of the triangle. Classifying them we get a translation (by a vector BC), two rotations (by ±120°) about C and R and the compositions of the translation with the reflections, giving one reflection (in CR) and two glide reflections (in PT and QS).

  6. If ΔABC and ΔA'B'C' are congruent "in the same sense" then they are related by a direct symmetry.
    If A ↦ A' under a rotation about a point P then P lies on the perpendicular bisector of AA'. Hence the three perpendicular bisectors would be coincident at P.
    If the triangles were related by a translation then the three perpendicular bisectors would be parallel.
    If the triangles were related by a glide reflection or reflection, then the midpoints of AA', BB' and CC' would all lie on the "mirror line".