Solutions 3

1. If f₁ = Rot_a,α and f₂ = Rot_b,β then f₁∘ f₂ is a translation if and only if α = -β.
   To prove that, write f₁ = T_a ∘ L ∘ T_-a and f₂ = T_b ∘ L' ∘ T_-b and note that if α = -β then L' = L ^-1.
   Then f₁∘ f₂ = a + L(-a + b + L ^-1(-b + x)) = a + L(b - a) - b + x which is translation by the vector a + L(b - a) - b

   If the lines meet then their intersection is a fixed point for the composition and so this is a rotation. If they are parallel the product is a translation by twice the distance between them.

   A glide reflection f is T_a ∘ R_l = R_l ∘ T_a.
   So the product f₁∘ f₂ = (T_a ∘ R_l) ∘ (T_b ∘ R_m) = T_a ∘ (R_l ∘ R_m) ∘ T_b and so is a rotation if the lines l, m meet (by twice the angle between them) and a translation if they are parallel.

2. The product of a rotation and reflection is either a reflection or a glide reflection. If a ∈ l then there is a fixed point and we have a reflection.
   If a l, then write the rotation about a as the product of reflection in a line m parallel to l and reflection in a line n.
   So f = R_l ∘ Rot_a = R_l ∘ R_m ∘ R_n = T_b ∘ R_n where b is a vector perpendicular to l. Thus since b is not perpendicular to n, this is a glide reflection by the lemma proved earlier.

3. It is easy to verify that H_a/2 ∘ H₀ = T_a.
   As in the last question, the condition is that a ∈ L.
   Note that H₀ is the map x 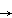-x and so H_a maps a + x to a - x.
   So acting on a - b + c with H_c maps it to -a + b + c and then acting on this with H_b gives a + b - c and acting on this with H_a gives a - b + c again. So this is a fixed point and since the composition of three half-turns is rotation by 3π which is the same as π the result is a half-turn about this point.

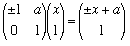4. Note that and so this matrix maps the line y = 1 to itself. Identifying this matrix with the isometry f(x) = ±x + a gives the isomorphism with I(R).
   Similarly the matrix 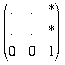acts on a vector f the form 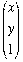to give another such vector. Hence the matrix 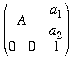corresponds to the isometry of R² given by T_a∘ L where a = (a₁, a₂) and A is the matrix of L ∈ O(2).

5. Look at the picture:

   Start with a pair of axes: 1 and 2 and follow their images under the glides.
   
   
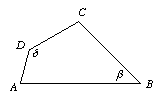   The composite of a pair of glides is a rotation (about some point) by twice the angle between them.
   So G_BC ∘ G_AB = rotation by 2β and G_DA ∘ G_CD = rotation by 2.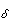
   So if 2β + 2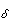 ≠ 2π the composite cannot be the identity.
   If β + 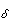= π then since A is fixed by the composite, we do have the identity.
   This is the condition that the quadrilateral is cyclic (the four vertices lie on a circle).

6. If h, k are either direct or opposite, so are their inverses and so composing h ∘ k ∘ h ^-1 ∘ k ^-1 gives a direct symmetry.

   If h, k are both rotations then their inverses are rotations by the opposite amount and so (by Question 1 above) when we compose we get a translation. The same thing happens if one is a translation. If both are translations, they commute and we have the identity.

   If f is a rotation about a by θ then take h, k to be reflections in lines meeting at a at an angle of α. Then f ∘ g is rotation by 2α and since h = h ^-1 and k = k ^-1 we have h ∘ k ∘ h ^-1 ∘ k ^-1= rotation by 4α and so we may take α = θ/4.

   To get a translation by a, take h to be rotation by π about 0 and take k to be rotation by π about a/4.