MT4518/5818 2002/3

Solutions 5

1. The dual of the rhombic dodecahedron has 6 square faces and 8 triangular faces. It is the cuboctahedron.

   The dual of the truncated octahedron has 24 triangular faces which careful consideration shows to come together to form 12 rhomboidal faces and so the dual is the rhombic dodecahedron.

   The truncated octahedron and and the rhombic dodecahedron are particularly important because copies of them can be used to fill up R³ without any gaps. Consequently, they appear "in nature" as crystals of various chemical compounds. With the obvious exception of the cube, none of the other Platonic solids can do this.

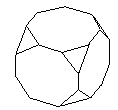2. The stella octangula has 24 faces, 8 vertices with 3 incident edges and 6 vertices with 8 incident edges. Hence its dual solid has 24 vertices, 8 triangular faces and 6 octagonal faces. It is a truncated cube:
   
   
   Hence the symmetry groups of the stella octangular are the same as those of the cube/octahedron.
   S_d ≅ S₄ and S ≅ S₄ × < J > .

   Colouring the two tetrahedra differently reduces the symmetry groups to those of the tetrahedron: S_d ≅ A₄ and S ≅ S₄.
   Colouring the top and bottom of the dual truncated cube differently from the others will give a figure whose rotational symmetry group S_d ≅ D₄ (the rotational symmetries of the square half-way up) and whose full symmetry group is S ≅ D₄ × < J > .
   Colouring the upper and lower faces or edges of the stellar octangula will have the same effect.

3. The direct symmetry group S_d(F) is the same as the group of rotational symmetries of the triangle half-way along and so is D₃ . Since J is not a symmetry of F and F does have some non-rotational symmetries, the full symmetry group of F is a mixed group and the only possibility is D₆D₃ .

   The direct symmetries of F₁ are the rotational symmetries of the "mid-rhombus" and hence the group S_d(F₁) ≅ D₂ .
   Since J is a symmetry of F₁ the full symmetry group S(F₁) ≅ D₂ × < J > .

   Any rotational symmetry of F₂ must be a rotational symmetry of the horizontal square and the only possible ones are rotation by π about a vertical axis through the centre or rotation by π about either of the diagonals.
   Hence S_d(F₂) ≅ D₂ .

   Since J is not a symmetry of F₂ but F₂ does have some opposite symmetries, the full symmetry group is a mixed group and hence we have S(F₂) ≅ D₄D₂ .

4. As in the last question, the direct symmetries of P_n are the rotational symmetries of the regular n-gon (or dihedron, if you like) half-way down the prism. This is the same as the full symmetry group D_n of the regular n-gon in R² (where the elements of order 2 are reflections rather than rotations by π).
   If n is even, then P_n is centrally symmetric (and has x ↦ -x as a symmetry) and so the full symmetry group is D_n × < J > . If n is odd, then, as in the last question, the full symmetry group is the mixed group D_2nD_n .

   The rotational group of the square antiprism consists of 4 rotations about the line joining the centres of the squares (including the identity!) and 4 rotations by π about lines joining the centres of opposite triangles.
   The group S_d ≅ D₄ .
   (If you cut the antiprism by a plane halfway up you get a regular octagon and some of the symmetries of this are symmetries of the solid.)
   The square antiprism is not centrally symmetric and so its full symmetry group is a mixed group which must be D₈D₄ .