Solutions 6

1. The direct symmetries or rotations of the tetrahedron map to the elements of A₄ × {I} ⊆ S₄ × < J >.
   The opposite symmetries of the tetrahedron map to symmetries of the cube of the form P × J where P is an odd permutation in S₄.
   The kernel of the map is trivial.

2. All the opposite symmetries of the dodecahedron are rotatory inversions. That is, they are of the form J ∘ R with R a rotation.
   Hence by Exercises 4 question 4 they are all rotatory reflections. The only ones which are actually reflections are those of the form J ∘ H with H a half turn and the only half-turns which are rotatory symmetries of the dodecahedron have axes joining the centres of pairs of opposite edges.
   There are 15 such pairs and the reflections are then in the planes through the mid-points perpendicular to these pairs of edges.

3. The groups C₂ , C₁ × < J > , C₂ C₁ are all cyclic groups of order 2.
   However, C₂ is generated by a half turn H, C₁ × < J > is generated by central inversion J , while C₂ C₁ is the mixed group generated by J ∘ H which is reflection in a plane.
   Hence these three are not conjugate in I(R³).

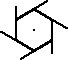4. To get a figure with rotation group C_n and no opposite symmetries paint a symbol like (but with n "arms") with only rotational symmetry on the bottom face of a pyramid on a regular n-gon.
   Painting the same figure on the top and bottom faces of an n-prism will give a figure with rotation group D_n and no opposite symmetries.
   Paint a (suitable situated) 3-armed version of this figure on each face of a tetrahedron, octahedron or icosahedron to get figures with the requisite rotation groups but no opposite symmetries.

   For figures with full symmetry group D_n × < J > take either a prism (n even) or an anti-prism (n odd).
   Paint the above symbol on the top and J(this symbol) on the bottom to get a figure with full symmetry group C_n × < J >.
   The stella-octangula, cube and dodecahedron give examples of centrally symmetric figures with direct symmetry groups of the Platonic figures.

5. The mixed group D_n C_n consists of n rotations (by multiples of 2π/n about the same axis) and n opposite symmetries of the form J ∘ H with H a half turn, which are reflections in planes containing this axis.
   Suitable figures include a right pyramid on a regular n-gonal base or an n-prism with its top surface painted a different colour.

   Choose a figure with full symmetry group D_n × < J > . (Either a prism or anti-prism depending on the parity of n.) Then mark a symbol like with only rotational symmetry on the top face and J(this symbol) on the bottom face.
   This figure will then have C_n × < J > as its full symmetry group.

   Similarly, when the full symmetry group of the prism/anti-prism is the mixed group D_2n D_n marking such symbols on the upper and lower n-gons will give a figure whose full symmetry group is C_2n C_n.

6. 1. Position a corner to see that for the direct symmetry group we have |S_d| = 4.
      The direct symmetries are the same as the direct symmetries of the rectangle where the tiles meet and so S_d = D₂ .
      Since the figure has central symmetry, the full symmetry group is S_d × < J > = D₂ × < J >.
      
   2. Again |S_d| = 4 and S_d = D₂ (the identity and rotation by π about three mutually perpendicular axes). This time the figure is not centrally symmetric but it does have some opposite symmetries. So the full symmetry group is a mixed group and the only possibility is D₄D₂ .
      
   3. As before S_d = D₂ but this time there are no opposite symmetries and so the full symmetry group is also D₂ .
      
   
   Colouring the tiles removes some of the possible symmetries. We get :
   
   1. S_d = C₂ and S = D₂C₂ since there is now no central symmetry.
      
   2. S_d = C₂ and S = D₂C₂
      
   3. S_d = C₂ and S = C₂
      
   
   

7. A half-turn about an axis joining the centres of opposite edges gives a transposition of the diagonals. So these 6 elements correspond to odd permutations. The other odd permutations (all 4-cycles) correspond to 6 rotation about centres of faces by ±π/2. All the other symmetries correspond to even permutations.

   Mapping the group of the cube to S₆ rotations by ±π/2 about face centres map to 4-cycles. Rotations by 2π/3 about diagonals map to cycles of the shape ( . . . )( . . . ). Half turns about diagonals or axes joining edge centres map to cycles of the shape ( . . )( . . )( . . )