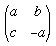Solutions 8

1. Either compose the function with itself or square the matrix representing the element to see that this element has order 2.

   A point x is a fixed point if x = (ax + b)/(cx - a) ⇒ cx² - 2ax - b = 0 ⇒ x = [a ± 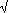(a² + bc)]/c and thus f has two fixed points equidistant from a/c = f(∞).

   Since f preserves cross-ratios (p , q ; x , f(x)) = (f(p) , f(q) ; f(x) , f²(x)) = (p , q ; f(x) , x) since p, q are fixed and f² = id.

   if γ = (a , b ; c , d) = (a , b ; d , c) then (d - b)/(d - a).(c - a)/(c - b) = (c - b)/(c - a).(d - a)/(d - b) ⇒ γ² = 1 ⇒ γ = ±1 and since x ≠ p, q we have γ ≠ 1. Hence γ = -1.

2. 
   Choose any point not on the first line l and join it to the first three points. Put in the second line m and adjust it so that two of the points are on the correct line. Then tilt it until the third point lies on the correct line.

   In fact the converse of this result is true: any map from RP¹ to RP¹ given by projection from a point not on either line does give an element of PGL(2, R).
   
   
   

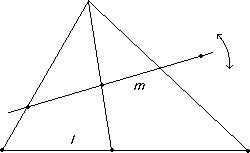
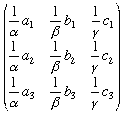3. If the first three points are a, b and c with homogeneous coordinates [a₁ , a₂ , a₃], etc. then the map given by the matrix maps the three given points to a, b and c.

   To map [1, 1, 1] to the fourth point means solving the equations ^a₁/_α + ^b₁/_β + ^c₁/_γ = 1, etc for ¹/_α, ¹/_β and ¹/_γ and we can do this since the matrix of coefficients is non singular (otherwise a, b and c would be on a line).

   Then, as in the case of RP¹, if θ maps these four standard points to a, b, c and d and φ maps them to a', b', c' and d' then the map we need is φ ∘ θ^-1.

4. The map x ↦ ¹/_(1-x) maps ∞ ↦ 0, 1 ↦ ∞ and 0 ↦ 1.
   Then conjugate this map by a map which maps a, b, c to ∞, 0, 1.

5. If x = [x, y] are homogeneous coordinates then x represents a fixed point of f if and only if Ax = λx for some λ ≠ 0. Note that since A ∈ GL it cannot have a 0 eigenvalue.

   The matrix 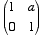has a unique eigenvector which represents the point at ∞. On the affine line the translationn T_a is x ↦ (1x + a)/1 = x + a and so is a translation.

   If g is any projective map with a unique fixed point p, let h be a map which sends p to ∞. Then h^-1∘g∘h has ∞ as a unique fixed point and so is a translation.

6. This follows since projection from a point leads to a projective transformation and these preserve cross-ratios.

7. 
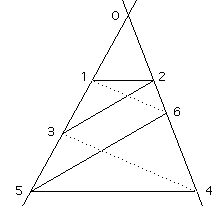
   Project P and Q to points on the line at infinity. This then gives a diagram:

   Then 12 ‖ 54 and 23 ‖ 65 and we need to show that 16 ‖ 34.
   To show this, prove that Δ016 and Δ034 are similar.

   To do this note that (by similar triangles) 01 : 05 = 02 : 04 and 03 : 05 = 02 : 06
   So 01 . 04 = 02 . 05 = 03 . 06 and so 01 : 03 = 06 : 04 which is what we need.
   
   

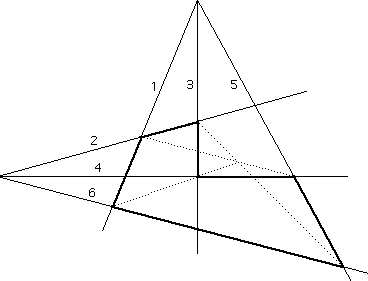8. The dual of Pappus's theorem is:

   If the alternate sides of a hexagon pass through two points then the joins of opposite vertices are concurrent.

   The diagram on the right illustrates this.