Remarks
- The remainder is smaller than the divisor. In Z we measure "size" by absolute value.
- Note that in fact there is a choice of remainders: you can either take it to be positive or negative.
Definition
The greatest common divisor (or highest common factor) of two integers a, b ∈ Z is the largest integer which divides them both.
Remarks
- We measure the "largeness" using the absolute value.
- The gcd is only unique up to multiplication by ±1. These are the invertible elements or units of Z.
We can use the division algorithm to prove
The Euclidean algorithm
If d is the gcd of a, b there are integers x, y such that d = ax + by.
Proof
Here is an example: Take a = 76, b = 32 :
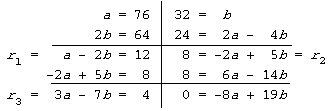
In general, use the procedure: divide (say) a by b to get remainder r1. Note that one can write r1 in terms of a and b.
Then divide b by r1 to get remainder r2. Note that one can write r2 in terms of b and r1 and hence in terms of a and b.
Repeat the process getting smaller and smaller remainders r1 , r2 , ... which must eventually lead to a remainder of 0.
At each stage ri can be expressed in terms of a and b. the last non-zero remainder d divides all the previous ones and hence both a and b. Hence it divides gcd(a, b). Since d can be written in terms of a and b the gcd(a, b) divides d and must therefore be ±d.

As a consequence of this algorithm we can now prove:
Theorem
Every ideal of Z is principal.
Proof
Let I be a non-zero ideal. Choose the smallest (non-zero) element a in the ideal I. If b is any other element then the gcd(a, b) is in I and this must be either ±a. So b is a multiple of a.
Thus I = < a > .
We now prove similar results for another ring.
The division algorithm for R[x]
If a(x), b(x) ∈ R[x] with b(x) ≠ 0 then ∃ q(x), r(x) ∈ R[x] such that a(x) = b(x)q(x) + r(x) with either r(x) = 0 or deg(r(x)) < deg(b(x)).
Remarks
- Note that this is almost word-for-word the same as the Z case.
- The remainder is smaller than the divisor. In R[x] we measure "size" by the degree.
Proof
We use the (slightly less well-known) process of dividing one polynomial by another (of lower degree). It is just like long division.
One example will suffice!
Take a(x) = 3x4 + 2x3 + x2 - 4x + 1 and b = x2 + x + 1
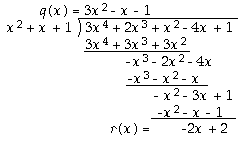

Definition
The greatest common divisor of two polynomials a(x), b(x) ∈ R[x] is a polynomial of highest degree which divides them both.
Remarks
- This is the largest polynomial dividing both where we measure the "largeness" using the degree.
- The gcd is only determined up to multiplication by a non-zero real number. These are the invertible elements or units of R[x].
- Note that if you calculate the gcd of (say) 2 and 4 as polynomials you get the answer 1, while as integers the result is 2.
One can then prove:
The Euclidean algorithm for polynomials.
If d(x) is the gcd of a(x), b(x) there are polynomials p(x), q(x) such that d = a(x)p(x) + b(x)q(x).
Proof
Just the same as for Z -- except that the divisions are more tedious.
Remarks
In the calculating package Maple the integer gcd is implemented with igcd and the Euclidean algorithm with igcdex. For polynomials use gcd and gcdex.
The above result on principal ideals follows for this ring.
Every ideal of R[x] is principal.
Proof
Just as in the Z case, an ideal is generated by its smallest (in degree) element.
Remarks
- An integral domain in which every ideal is principal is called a principal ideal domain or PID.
- The results about the real polynomials above can be proved for the ring of polynomials F[x] over any field F. What we have just proved is that: F[x] is a PID.
Now let us prove the same result for a completely different ring.
Definition
The ring of Gaussian integers is the subring {a + bi | a, b ∈ Z} of C. It is denoted Z[i].
We'll prove the division and Euclidean algorithms for this ring but first we have to decide when one Gaussian integer is bigger or smaller than another.
Definition
The norm (or length) of the Gaussain integer a + bi is a2 + b2. We will write it as N(a + bi).
Remarks
- This is, of course, |z|2 with z = a + bi. It is more convenient not to take the square root, since it keeps the norm as an integer.
- If u, v are Gaussian integers, the norm satisfies N(uv) = N(u)N(v).
The division algorithm for Z[i]
If u, v ∈ Z[i] with v ≠ 0 then ∃ q, r ∈ Z[i] such that u = vq + r with N(r) < N(v).
Remarks
- The remainder is smaller than the divisor. In Z[i] we measure "size" by the norm.
- We will see that in fact there is sometimes a choice of remainders.
Proof
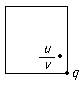
This proof is very different to the other proofs above.
First divide u by v in C. You get a complex number u /v which lies in one of the "cells of the integer lattice".
At least one corner of the square is within distance 1 of u/v. This is the quotient q. The remainder is then r = u - vq and since |u/v - q| < 1 we have |u - qv| < |v| and so N(r) < N(v) as required.
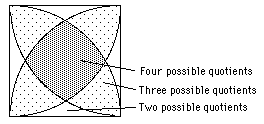
Remark
For most positions of u/v there will be a choice of 2, 3 or even four Gaussian integers for the quotient.
Definition
The greatest common divisor of two Gaussian integers u, v ∈ Z[i] is a Gaussian integer of largest norm which divides them both.
Remarks
- Note that we measure the "largeness" using the norm.
- The gcd is only determined up to multiplication by an invertible Gaussian integer. These units of Z[i] are ±1 and ±i.
Then we can calculate just as before and prove:
The Euclidean algorithm for Gaussian integers.
If w is the gcd of u, v there are Gaussian integers g, h such that w = ug + vh.
and then we can deduce:
Every ideal of Z[i] is principal.
Remark
A ring in which one can define a sensible notion of size which leads to a Euclidean algorithm is called a Euclidean ring.
| Previous page (Subrings and ideals) | Contents | Next page (Ring homomorphisms and isomorphisms ) |