Rings and Fields
Ring homomorphisms and isomorphisms
Just as in Group theory we look at maps which "preserve the operation", in Ring theory we look at maps which preserve both operations.
Definition
A map f : R→ S between rings is called a ring homomorphism if
f(x + y) = f(x) + f(y) and f(xy) + f(x)f(y) for all x, y ∈ R.
Remarks
- The operations on the left are in the ring R; those on the right are in S.
- Since such a homomorphism is a group homomorphism from (R, +) to (S, +) it maps 0R to 0S.
Even if the rings R and S have multiplicative identities a ring homomorphism will not necessarily map 1R to 1S.
- It is easy to check that the composition of ring homomorphisms is a ring homomorphism.
Definition
A ring homomorphism which is a bijection (one-one and onto) is called a ring isomorphism.
If f : R → S is such an isomorphism, we call the rings R and S isomorphic and write R 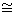 S.
S.
Remarks
- Isomorphic rings have all their ring-theoretic properties identical. One such ring can be regarded as "the same" as the other.
- The inverse map of the bijection f is also a ring homomorphism.
Examples
- The map from Z to Zn given by x ↦ x mod n is a ring homomorphism. It is not (of course) a ring isomorphism.
- The map from Z to Z given by x ↦ 2x is a group homomorphism on the additive groups but is not a ring homomorphism.
- The map from Z to the ring of 2 × 2 real matrices given by x ↦
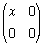 is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity.
is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity.
Of course the map x ↦ x mod n is a homomorphism which does map the identity to the identity.
- The "evaluation at 1/2 map" from the ring of continuous real-valued functions on the interval [0, 1] to R given by (e½)f = f (1/2) for f belongs C[0, 1] is a ring homomorphism.
- The "evaluation at 1 map" from the ring Q[x] to Q given by (e1)p = p(1) for p ∈ Q[x] is a ring homomorphism.
That is: e1(a0 + a1x + a2x2 + ... + anxn) = a0 + a1 + a2 + ... + an.
- The "evaluation at √2 map" from Z[x] to R given by p ↦ p(√2) is a ring homomorphism.
This will turn out to be a surprisingly important example.
- The map from C to ring of 2 × 2 real matrices given by a + bi ↦
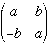 is a ring isomorphism.
is a ring isomorphism.
Proof: Exercise.
- Let R be the field with 9 elements {a + bx | a, b ∈ Z3} and the multiplication rule x2 = -1.
Let S be the field with 9 elements {a + by | a, b ∈ Z3 } and the multiplication rule y2 = y + 1.
Then the map defined by 1 ↦ 1 and x ↦ y + 1 defines a ring isomorphism.
Proof: We'll see a neat way of proving this later.
The connection of this with the last section is given by:
Definition
The kernel of a (ring) homomorphism is the set of elements mapped to 0.
That is, if f: R→ S is a ring homomorphism, ker(f) = f-1(0) = {r ∈ R | f(r) = 0S }.
Theorem
The kernel of a ring homomorphism is an ideal.
Proof
An easy verification.
Remarks
- Note the similarity with the corresponding result for groups: the kernel of a group homomorphism is a normal subgroup.
- If the ring R is not commutative, the kernel is a two-sided ideal.
Examples
- The kernel of the above map from Z to Zn is the ideal nZ.
- Just as in the group-theory case, the kernel of a homomorphism is {0} if and only if the homomorphism is one-one.
Proof
(=>) If f(r) = f(s) then f(r - s) = 0 and so r - s belongs ker(f) and we have r - s = 0.
(<=) If a ∈ ker(f) and a ≠ 0 then a, 0 ↦ 0 and so the map is not one-one.
- The kernel of the "evaluation at 0" map from R[x] to R is the ideal < x > of polynomials with zero constant terms.
- The kernel of the "evaluation at 0 taken modulo 2" map from Z[x] to Z2 is the ideal < 2, x > of polynomials with even constant terms.
Remark
We will see later that every ideal is the kernel of a ring homomorphism. This is similar to the group theory result that every normal subgroup is the kernel of a group homomorphism.
The last result in this section also parallels the corresponding example in Group theory,
Theorem
The image of a ring homomorphism f: R→ S is a subring of S.
Proof
The image is the set im(f) = {s ∈ S | s = f(r) for some r ∈ R }. It is easy to do the verification.
Example
The image of e√2 from Z[x] to R is the subring {a + b √2 | a, b ∈ Z } we met earlier.
JOC/EFR 2004
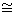 S.
S.
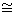 S.
S.
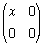 is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity.
is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity.
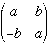 is a ring isomorphism.
is a ring isomorphism.





