Factor rings and the isomorphism theorems

We parallel the development of factor groups in Group theory.

Definition

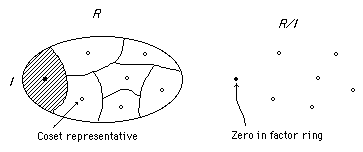
If I is an ideal of a ring R and a ∈ R then a coset of I is a set of the form a + I = {a + s | s I }.

The set of all cosets is denoted by R/I.

Remarks

1. This is the same as the (additive) group theoretic coset. As in the groups case the cosets partition the ring into disjoint subsets.

2. The element a is called a coset representative of the coset. Note that each coset will have lots of coset representatives. Elements a₁ and a₂ represent the same coset of I if a₁ - a₂ ∈ I.

3. The ideal I is itself a coset : 0 + I.
   

Theorem

If I is an ideal of a ring R, the set R/I is a ring under the operations

(a + I) + (b + I) = (a + b) + I and (a + I) . (b + I) = (ab) + I.

Proof

We need to check that the operations are "well-defined". That is if a₁ and a₂ are representatives of the same coset and b₁ and b₂ represent the same coset then a₁ + b₁ and a₂ + b₂ represent the same coset and so do a₁b₁ and a₂b₂.

We have a₁ - a₂ I and b₁ - b₂ I and so adding these shows that (a₁ + b₁) - (a₂ + b₂) ∈ I and so these do represent the same coset.

Similarly, for the product, observe that a₁b₁ - a₂b₂ = (a₁ - a₂)b₁ + a₂(b₁ - b₂) and the result follows from the properties of the ideal.

Once you know that the operations are well-defined the ring axioms follow easily.

Note that the zero of the factor ring is the coset 0 + I or the ideal I itself.

Remarks

1. We call this ring a factor ring rather than a quotient ring to avoid confusion with something called a "ring of quotients".

2. The way you should think of the factor ring R/I is that it is the ring R in which "all the elements in the ideal I have been made into zero". This is sometimes called "killing of the elements of I".

3. Here is a "picture":

Examples

1. Let I = nZ ⊆ Z.
   Then Z/nZ has n elements: I, 1 + I, 2 + I, ... , (n - 1) + I and the factor ring is Z_n.

2. Let I be the ideal of R[x] generated by the polynomial x² + 1.

   Then every coset has a representative of the form (a + bx) + I since if we choose a coset representative (say) x³ then we have x³ = -x + (x² + 1)x - x + I and so -x will do for a representative instead. You should see that by thinking of x² + 1 as 0 one can use the "rule" x² = -1 to get rid of all higher powers.

   So we get a ring in which we can add and multiply things like a + bx using the rule x² = -1 to do multiplication.

   If you replace the indeterminate x by i you will see that this is the complex numbers.

   That is: R[x]/ < x²+ 1 > C .

3. Using a similar argument we can see that the finite field GF(9) constructed earlier is in fact the factor ring Z₃[x]/< x² + 1 > since the "multiplication rule" x² = -1 we used is equivalent to x² + 1 = 0.

4. The ring Z₅[x]/< x² + 1 > has 25 elements since (as above) coset representatives can be chosen to be of the form a + bx with a, b ∈ 5. However, this is not a field since the cosets (x + 3) + I and (x + 2) + I have a product (x + 3)(x + 2) + I = 0 + I. Hence the ring has zero-divisors and is not a field.

   Notice that the reason that this happened was that the polynomial x² + 1 factorises in Z₅[x] into a product of factors of lower degree. (You could see it had linear factors since the polynomial has roots in 5.)
   

We saw in the last section that the kernel of a ring homomorphism is an ideal and the image is a subgroup. In view of the corresponding result for groups it will come as no surprise that we have

The Isomorphism Theorem for Rings

If f :R→ S is a ring homomorphism the factor ring R/ker(f) is isomorphic to im(f).

Proof

Define the map θ: R/ker(f)→ im(f) by θ(a + ker(f)) = f(a).

Then the proof is exactly as in the group theory case except you also need to check that this map respects the ring multiplication as well as addition.

Remarks

1. This shows that one can always think of factor rings as "homomorphic images" rather than as something involving operations of subsets (cosets).

2. From this theorem every ideal is the kernel of some homomorphism (the map from R to R/I).

The above result is sometimes called the First Isomorphism Theorem for Rings. Here are some others.

The Second Isomorphism Theorem for Rings

Let I and J be ideals of a ring R. Then I + J and I ∩ J are also ideals and the factor rings (I + J)/J and I/(I ∩ J) are isomorphic.

Proof

Here is a picture showing the inclusions. The double lines represent the two factor rings.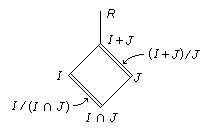

To prove the result, Define θ : I→ (I + J)/J by i ↦ i + J.

Since every coset in (I + J)/J has a representative of this form θ is onto.

If i ∈ ker(θ) then i + J = J and so i ∈ J and hence is in I ⊆ J.

The result now follows from the First Isomorphism Theorem.

Remark

In fact one only needs I to be a subring of R for this theorem to hold. One does need J to be an ideal.

Example

Let I = < m > and J = < n > be ideals of Z. Then (See Exercises 4 Qu 1) I + J = < gcd(m, n) > and I ∩ J = < lcm(m, n) > .
Then from this theorem one deduces that < gcd(m, n) > / < n > 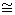< n > / < lcm(m, n) > and from this you may deduce that n/gcd(m, n) = lcm(m, n)/m or that gcd(m, n) × lcm(m, n) = mn (See Exercises 3 Qu 6).

The Third Isomorphism Theorem for Rings

Let I and J be ideals of a ring R with I ⊆ J. Then J/I is an ideal of R/I and (R/I)/(J/I) 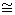R/J

Proof

It is easy to verify that J/I is an ideal of R/I.

Define a map θ : R/I→ R/J by a + I ↦ a + J for any coset a + I of I in R. This is clearly onto.

An element a + I is in the kernel of θ if a + I = J which (since I ⊆ J) will only happen if a ∈ J. Thus ker(θ) = J/I ⊆ R/I and the result follows from the the First Isomorphism Theorem.