The projective groups

Any invertible map T from a vector space V to itself leads to a bijection of the associated projective space P(V).
(Just map [u] [T(u)] where u are homogeneous coordinates.)
However, maps of the form λI for λ a non-zero scalar act as the identity on P(V).

Definition

If F is any field, the quotient group GL(n, F)/{λI | λ ∈ F - {0} } is called the projective group and is written PGL(n, F).
The elements of this group are called projective transformations or projectivities. (The name projection is used for something different.)

We will now look at some examples

The easiest (and most important) case is PGL(2, R).

This is the group which acts on P(R²) = RP¹: the real projective line.
In Klein's formulation it is the group of 1-dimensional real projective geometry.
Let 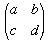represent an element of PGL(2, R). Note that 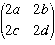etc. will represent the same element.
This acts on an ordinary point with homogeneous coordinates [x, 1] to give [ax + b , cx + d] or equivalently [(ax + b)/(cx + d), 1] provided that cx + d ≠ 0.
That is, the matrix corresponds to the rational map x 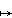(ax + b)/(cx + d) where we interpret this as ∞ if cx + d = 0. Note that we must have ad - bc ≠ 0 otherwise the map would not be invertible.
Looking at what happens to the point at infinity = [1, 0], this maps to ^a/_c (just as we might expect).

Remarks

1. One may prove that the composite of such rational maps corresponds to the multiplication of matrices.
   (Believe it or not this was the way that the English mathematician Arthur Cayley (1821 to 1895) first defined the multiplication of matrices).

2. Such projective transformations do correspond to projection from a point as seen earlier. (See Exercises 8 Question 3)
   

The following trick makes studying projectivities easier.

Definition

The standard reference points on RP¹ are ∞, 0 ,1 (that is [1, 0], [0, 1] and [1, 1]).

Theorem
There is a unique projective transformation taking any three distinct points to ∞, 0 ,1.

Proof
The map is x 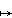(x - b)/(x - a) . (c - a)/(c - b).

Corollary
There is a unique projective transformation taking any three distinct points to any other three distinct points.

Proof
If the map θ maps a, b, c to ∞, 0 ,1 and φ maps a', b', c' to ∞, 0 ,1 then the map φ^-1θ does what is needed.

Projective maps do not preserve lengths or ratios or even intermediacy. However they do preserve something called cross-ratio.

Definition

Let a, b, c, d be four points of RP¹. Let θ be the map taking a, b, c to ∞, 0, 1. Then the cross-ratio (a , b ; c , d) is θ(d).

From the above this is (a , b ; c , d) = (d - b)/(d - a) . (c - a)/(c - b).

Remarks

1. Drawing the points on a line:
   the cross ratio is the ratio in which C divides AB divided by the ratio in which D divides AB: that is (^AC/_CB)/(^AD/_DB).

2. If D is at infinity this is the ratio AC/BC ( = - AC/CB).

3. If the cross-ratio is -1, the four points are said to be harmonic.
   If D is at infinity then AC = CB for a harmonic range (as it is called).
   

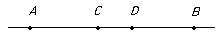
Proof
If f is a projective map and θ takes a, b, c to ∞, 0, 1 then θ f ^-1 takes f(a), f(b), f(c) to ∞, 0, 1. The cross ratio (a , b ; c , d) is θ(d) and this is the same as θ f ^-1(f(d)) and the result follows.