As in the last example the elements of this group can be regarded as the set of those rational analytic functions of the form:
z
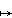 (az + b)/(cz + d) with a, b, c, d ∈ C with ad - bc ≠0,
(az + b)/(cz + d) with a, b, c, d ∈ C with ad - bc ≠0,from C ∪ {∞} to itself.
| Previous page (The projective groups) | Contents | Next page (Some theorems in plane projective geometry) |
The projective group PGL(2, C).
This is the group that acts on the complex projective line P(C2) = CP1.
As in the last example the elements of this group can be regarded as the set of those rational analytic functions of the form:
z 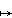 (az + b)/(cz + d) with a, b, c, d ∈ C with ad - bc ≠0,
(az + b)/(cz + d) with a, b, c, d ∈ C with ad - bc ≠0,
from C ∪ {∞} to itself.
Remarks
This is the group that acts on the real projective plane P(R3) = RP2.
One may show that there is a unique element of this group taking any four points in RP2 (no three on a line) into any other four points in RP2.
As in the projective line case, one may take standard reference points to be: [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 1]. These are the points at infinity on the x and y axes, the origin and the point (1, 1). We may manipulate these as in the earlier case.
We may define the cross-ratio of four points on a line and these transformations preserve that.
| Previous page (The projective groups) | Contents | Next page (Some theorems in plane projective geometry) |