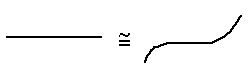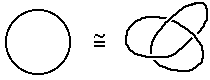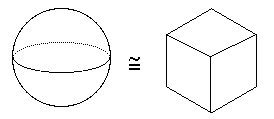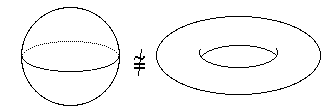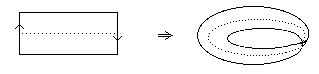Course MT4521 Geometry and topology
Introduction to topology
Topology is (roughly) the study of properties invariant under "continuous transformation".
More formally:
Let S, T be sets with a structure for which the idea of continuity makes sense. e.g. Subsets of Rn, metric spaces, ...
Then a bijection f from S to T is called a homeomorphism or topological isomorphism if both f and f-1 are continuous. We then write S 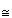 T.
T.
In Klein's formulation, the set of all such maps from a space to itself is a group and topology is the associated geometry.
Examples
- A line and a curve are homeomorphic:
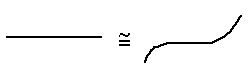
- A circle S1 and a knot K (subsets of R3) are homeomorphic -- even though one cannot be deformed into the other (in R3).
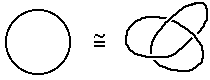
Strangely, R3 - S1 and R3 - K are not homeomorphic.
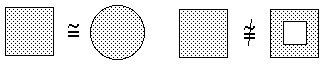
- A closed (including its boundary) disc and closed unit square are homeomorphic.
- A sphere (the surface) and the surface of a cube are homeomorphic.
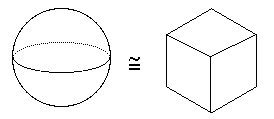
"Proof"
Put the cube at the centre of the sphere and project from the centre.
- A sphere and a torus are not homeomorphic.
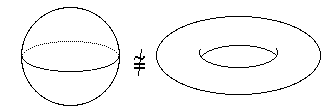
"Proof"
Removing a circle from a sphere always splits it into two parts -- not so for the torus.
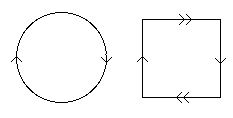
- A cylinder S1 × I and the space made by gluing a strip after a full turn are homeomorphic -- even though (cf example 2) one cannot be deformed into the other.
- The Möbius band is a "space" made by gluing together the ends of a strip after a half turn.
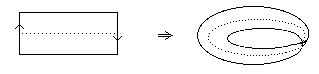
- The Real projective plane RP1 = {the set of lines through 0 in R3}
If we take an "upper hemisphere", this meets each line in a unique point which we may take as the representative of that point of the projective plane -- except for opposite points on the equator which have to be "identified". 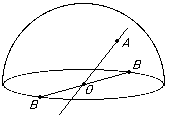
Hence the Real Projective Plane can be regarded as a disc which opposite points on its boundary identified.
JOC February 2010
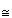 T.
T.