| Previous page (Introduction to topology) | Contents | Next page (The Connected Sum) |
Most of the above examples are surfaces.
Definition
A surface is something in which every point has a region around it which is homeomorphic to a disc in R2.
We will be most interested in what are called compact surfaces. These are closed (in the sense that they contain the limits of all sequences in them) and bounded subsets of Rn.
Examples
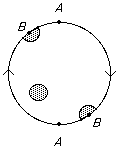
See the above examples: a Sphere S2, a Torus T, an (open) cylinder (which does not contain the upper and lower boundary circles and so is not compact), an (open) Möbius band (with the boundary removed -- so it is not compact either) and the Real Projective Plane.
The see how each point of the Projective Plane has the "right kind" of region around it, piece together the area around a boundary point B from "two bits". 
More examples
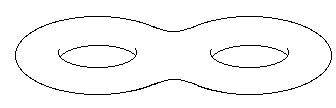
More generally, one can construct an n-holed torus or "surface of genus n".
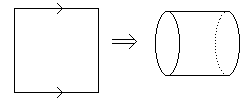
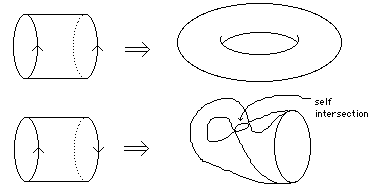
Making the Klein bottle corresponds to identifying the edges of the square as: 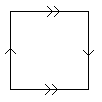
| Previous page (Introduction to topology) | Contents | Next page (The Connected Sum) |