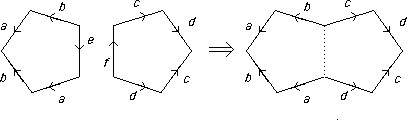Planar models

To work with more complicated surfaces we use a more systematic way of describing how to make them.

Definition
A planar model of a compact surface is a disc whose boundary is a 2n-gon whose edges are identified in pairs.

Remarks

1. If we have a polygon with some unidentified edges then this represents a surface with some "free edges" (and not compact).
   
2. We can describe the planar model by labelliing the edges with letters and choosing a direction to go round the boundary and then reading off the edges as we go: putting an inverse on any edge we meet in the "opposite direction". This gives an edge-word for the planar model.
   

1. For the torus we have 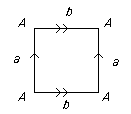with edge word aba^-1b^-1
   Note that all four corners of the square get identified to the same point.
   
2. For the Klein bottle we have 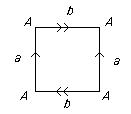with edge word aba^-1b
   Again all four corners of the square get identified to the same point.
   
3. For the Projective Plane we have 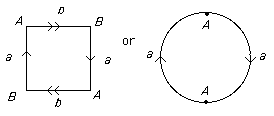with edge word abab or a²
   In this case the corners of the square get identified to a pair of points.

4. A cylinder has edge word aba^-1c and the Möbius band has edge word abac

5. When we make a 2-holed torus we remove discs from tori with edge words aba^-1b^-1 and cdc^-1d^-1 to get surfaces with holes: aba^-1b^-1e and cdc^-1d^-1f which we then join together to get a model with planar word aba^-1b^-1cdc^-1d^-1
   
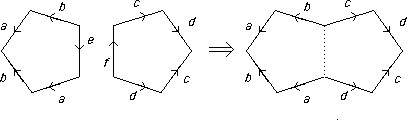
   More generally:

   Given planar models for surfaces S₁ and S₂ with edge words w₁ and w₂ , the edge word of a planar model for the connected sum is the concatenation w₁w₂ .

6. The Klein bottle (again)
   Joining two Projective Planes with edge words a² and b² gives a planar model with edge word a²b² which is different from that in example 2 above.
   However, one can manipulate as follows.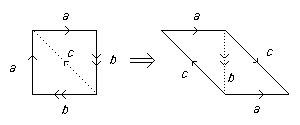
   So the edge word a²b² becomes aca^-1c which is equivalent to the one above.

   It follows that it may be hard to recognise what surface is represented by a given edge word.