The Euler Characteristic

The Euler Characteristic is something which generalises Euler's observation of 1751 (in fact already noted by Descartes in 1639) that on "triangulating" a sphere into F regions, E edges and V vertices one has V - E + F = 2.

If one triangulates any surface then χ = V - E + F is a number which does not depend on how the triangulation is done. This is called the Euler Characteristic.

Examples

1. χ(Torus) = 0
   
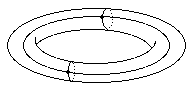
   For example we can split up the torus into "regions" (homeomorphic to discs) with F = 2, E = 4, V = 2 or even more efficiently as 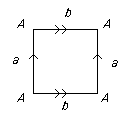    with F = 1, E = 2, V = 1
   
2. χ(Projective plane) = 1
   The planar model with edge word a² gives a triangulation with F = 1, E = 1, V = 1
   
3. χ(Klein bottle) = 0
   The model 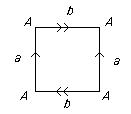gives a triangulation with F = 1, E = 2, V = 1
   

Corollary
For the join of n tori we have χ = -2(n - 1) and for the join of n Projective planes we have χ = -(n - 2).
Proof
Use induction and χ(T) = 0, χ(P) = 1.

So if we could recognise whether a surface could be written as a product of tori or of projective planes, the Euler characteristic would be enough to classify it.

Definition
If when we carry a direction around any loop in a surface we always get a consistent direction the surface is called orientable.

Examples

1. A sphere and any join of tori are orientable.
   Proof
   The direction of an "outward-pointing normal" can be used to define the direction.

2. A Möbius band is not orientable.
   Proof
   Carry a direction around the curve "in the middle of the band". (A normal at a point would come back pointing the opposite way after going round once.)

3. A Projective plane or any join of projective planes is not orientable.
   Proof
   These all contain a Möbius band.

4. Any surface whose planar model contains an edge which is identified with itself rather than its inverse is not orientable.
   Proof
   Cut a strip out of the model with ends on the identified edge and you have a Möbius band.