The Classification Theorem

This is one of the few examples in mathematics where such a complete classification of geometric objects is known.

The Classification Theorem
If a compact connected surface is orientable it is a sphere or a connected sum of tori; if it is not orientable it is a connected sum of projective planes.

Remarks

1. This was first proved by Dehn and Heergaard in 1907.

2. One proves this result by starting with any surface and using the result (the Hauptvermutung) that it can be triangulated to get a planar model. Then cut up the planar model and piece it together again until one can recognise it as a join of tori or projective planes. In general this is quite hard!

3. We use the Euler characteristic as a short cut since we can see whether the surface is orientable of not from its edge word. All we need is a method of calculating χ.
   

Given an edge word (a word of length 2n in n generators in which each edge is matched either by itself or its inverse.
If there is an edge matched by itself, the surface is not orientable, otherwise it is orientable.

So for such a surface, we have F = 1, E = n and all we need calculate is V: the number of vertices on the "edge".

We do this by a process similar to coset enumeration by starting with a single vertex somewhere and adding new vertices only when we have to.

Examples

1. Start with an edge word a b c d c^-1b^-1a^-1d^-1:     

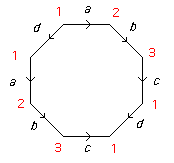
   Hence F = 1, E = 4 and V = 3. Hence χ = 0.
   Since the surface is orientable (every edge is matched with its inverse) it is a Torus T.

2. From the edge word: a b c d e c^-1 d^-1 b a e^-1 we can fill in the vertices:
   
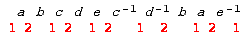
   and so we have: χ = 1 - 5 + 2 = -2
   Since the surface is not orientable, it is a join of Projective planes and from the Corollary it is P # P # P # P.
   

Remarks
This way of identifying a surface is much easier than dealing directly with the edge word.

For example joining a Torus and a Projective plane gives a non-orientable surface with χ = -1 which is therefore a connected sum of three projective planes -- though this is hard to see by other means.

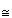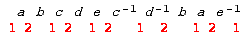
It follows that (Torus) # (Projective plane) (Klein bottle) # (Projective plane) but, of course the Torus and Klein bottle are not homeomorphic.