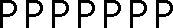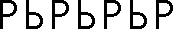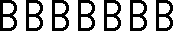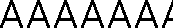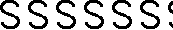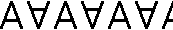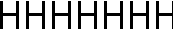Frieze groups

We now look at some infinite subgroups of I(R²).

We will look at subgroups which map a strip, say the subset R × [-1, 1], and are discrete. That is, there are no elements which move points an arbitrarily small distance.
[For example, the additive group of reals R acting on the line by addition is not a discrete group.]

The finite symmetry group of the strip is D₂. The elements of this group are: the identity I, a reflection R in the horizontal, a reflection V in a vertical line (through 0 say) and a half turn H (about 0 say).
We have R² = V² = H² = I , RV = VR = H etc.

What else could be in an infinite group?
It could contain a translation T (which we will take to be by a shortest distance in the group) and/or a glide reflection G (which we can take to be G = TR = RT).
We then get the following possible groups generated by some of these elements. In each case we give a pattern which is mapped to itself by the group.
(See Exercises 4 Question 3)

	Group generated by:	Pattern left invariant	Group
(i)	T	.... 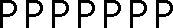....	C∞
(ii)	G	.... 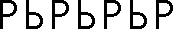....	C∞
(iii)	T, R	.... 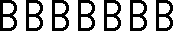....	C∞ × D1
(iv)	T, V	.... 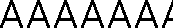....	D∞
(v)	T, H	.... 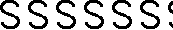....	D∞
(vi)	G, V	.... 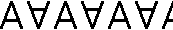....	D∞
(vii)	everything	.... 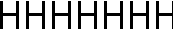....	D∞ × D1

These seven groups are the only possibilities -- up to conjugacy in the group I(R²).