Let X be a set. A set
 of subsets of X is called a topology (and the elements of
of subsets of X is called a topology (and the elements of  are called open sets) if the following properties are satisfied.
are called open sets) if the following properties are satisfied.| Previous page (Topological Motivation) | Contents | Next page (Properties of topological spaces) |
We now build on the idea of "open sets" introduced earlier.
Definition
Let X be a set. A set  of subsets of X is called a topology (and the elements of
of subsets of X is called a topology (and the elements of  are called open sets) if the following properties are satisfied.
are called open sets) if the following properties are satisfied.
 (the empty set), X
(the empty set), X 
 ,
, I}
I} 
 then
then 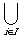 Ai
Ai 
 ,
,
 then A
then A  B
B 
 .
. is closed under arbitrary unions and finite intersections.
is closed under arbitrary unions and finite intersections. ) is called a topological space.
) is called a topological space. to be the set of open sets as defined earlier. The properties verified earlier show that
to be the set of open sets as defined earlier. The properties verified earlier show that  is a topology.
is a topology.
 = {
= { , X}. Then
, X}. Then  is a topology called the trivial topology or indiscrete topology.
is a topology called the trivial topology or indiscrete topology. be the set of all subsets of X. The
be the set of all subsets of X. The  is a topology called the discrete topology. It is the topology associated with the discrete metric.
is a topology called the discrete topology. It is the topology associated with the discrete metric.
Remark
A topology with many open sets is called strong; one with few open sets is weak.
The discrete topology is the strongest topology on a set, while the trivial topology is the weakest.
 ={
={  , X, {a} }.
, X, {a} }.  is a topology called the Sierpinski topology after the Polish mathematician Waclaw Sierpinski (1882 to 1969).
is a topology called the Sierpinski topology after the Polish mathematician Waclaw Sierpinski (1882 to 1969).
Let X = {1, 2, 3} and  = {
= { , {1}, {1, 2}, X}. Then
, {1}, {1, 2}, X}. Then  is a topology.
is a topology.
Remark
It is easy to check that the only metric possible on a finite set is the discrete metric. Hence these last two topologies cannot arise from a metric.

 if X - A is finite or A =
if X - A is finite or A =  .
.
 = {
= { , R}
, R} 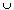 { (x,
{ (x,  ) | x
) | x  R}
R}  is a topology in which, for example, the interval (0, 1) is not an open set.
is a topology in which, for example, the interval (0, 1) is not an open set.
| Previous page (Topological Motivation) | Contents | Next page (Properties of topological spaces) |