Continuity for topological spaces

As previewed earlier whan we considered open sets in a metric space, we can now make the definition:

Definition
A map f: X Y between topological spaces is continuous if f ^-1(B) _X whenever B _Y.

Remark
Note that a continuous map f: X Y "induces" a map from _Y to _X by B 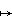f ^-1(B).

Definition
A map f: X Y between topological spaces is a homeomorphism or topological isomorphism if f is a continuous bijection whose inverse map f_-1 is also continuous.

Remark
By the remark above, such a homeomorphism induces a one-one correspondence between _X and _Y.

Examples

1. Let f be the identity map from (R², d₂) to (R², d). Then f is a homeomorphism.
   Proof
   Since every open set is a union of open neighbourhoods, it is enough to prove that the inverse image of an -neighbourhood is open. This -neighbourhood is an open square in R² which is open in the usual metric.
   A similar proof shows that the image of an -neighbourhood in the usual metric (an open disc) is open in d .
   
   
   
2. In general, if X is a set with two topologies ₁ and ₂ then the identity map (X, ₁) (X, ₂) is continuous if ₁ is stronger (contains more open sets) than ₂ .